5.1. Полиномы над кольцом.
Пусть R - некоторое кольцо.
Полиномом (или многочленом) над R от x называется
формальное выражение вида
Теорема.Пусть R -- кольцо. Тогда R[ x] --
кольцо. Если R
коммутативно, то R[x] коммутативно. Если R -- кольцо с 1, то
R[x] -- кольцо с единицей.
Доказательство. Непосредственнная проверка аксиом.
Предложение. Степень суммы многочленов не превосходит максимума
степеней слагемых. Степень произедения не превосходит суммы
степеней сомножителей. Если R -- кольцо с 1 и один из старших
коэффициентов сомножителей в произведении двух многочленов
обратим, то степень произведения равна сумме степеней
сомножителей и старший коэффициент произведения равен
произведению старших коэффициентов соможителей.
Доказательство -- по определению суммы и произведения.
5.2. Кольцо многочленов над полем. Деление с остатком.
До конца главы k будет обозначать некоторое поле. Из
теоремы и предложения предыдущего параграфа вытекает, что k[ x]
-- коммутативное кольцо с 1, степень произведения в кольце k[ x]
всегда равна сумме степеней сомножителей и старший коэффициент
произведения равен произведению старших коэффициентов
сомножителей. В частности, многочлен тогда и только тогда
обратим в кольце k[x], когда его степень равна нулю.
Теорема. Пусть
Доказательство. 1. Индукция по стg
. Если стf<
стg,
то f=0g+f
и h=0,r=f.
Пусть
теорема доказана для всех пар (f1,g)
, где
стf1<
стf
. Можно считать, что
5.3. Делители многочлена. Наибольший общий делитель.
Пусть
5.3.1. Упражнения. Доказать следующие утверждения для полиномов
над полем k:
1. Если
f делится на
g,
g делится на
h, то
fделится на
h.
2. Если полиномы
f1,...,fn
делятся на h
, то для любых полиномов
u1,...,un
полином
f1u1+...+fnun
делится на h.
3. Полином нулевой степени делит любой полином.
4. Если g
делит f
и степени g
и f
равны, то f = ag, где
5.3.2. Наибольшим общим делителем полиномов f и g называется
любой полином d, обладающий следующими двумя свойствами: а) d делит и
f, и g, б) d делится на любой полином, делящий и f, и g.
Пункт 5 упражнения 5.3.1. показывает, что два наибольших общих делителя двух
данных многочленов отличаются множителем нулевой степени и произведение
наибольшего общего делителя на многочлен нулевой степени снова является
наибольшим общим делителем тех же многочленов. В частности, если существует
наибольший общий делитель многочленов f и g, то существует и их (однозначно
определенный) наибольший
общий делитель, старший коэффициент которого равен 1. Этот наибольший общий
делитель обозначается символом (f,g).
Следующий результат показывает, что наибольший общий делитель всегда
существует, и дает алгоритм для его вычисления.
5.3.3. Теорема (алгоритм Евклида). Пусть
Доказательство. 1. Поскольку степень fn меньше степени
fn-1 для всех n, найдется натуральное число m (не превосходящее
степень полинома f2), что
5.3.4. Упражнение. Полиномы u1,u2 можно выбрать так, чтобы
степень ui была меньше
f3-i,i=1,2, и этим условием полиномы
u1,u2 определяются однозначно. Доказать.
5.4. Взаимно простые полиномы. Говорят, что полиномы f и
g взаимно просты, если (f,g)=1.
5.4.1. Теорема. Полиномы f и g взаимно просты
Доказательство.
5.4.2. Теорема. 1. Если
(f,gi)=1, i=1,2,...,r, то
Доказательство. 1. Достаточно доказать утверждение при r=2, а затем
получить общий результат тривиальной индукцией по r. По теореме 5.4.1
существуют такие полиномы
u1,v1,u2,v2, что
u1f+v1g1=1,
u2f+v2g2=1.
Отсюда
5.5. Неразложимые полиномы. Полином f называется разложимым в
k[x] (или над k),
если f=gh, где g,h -- полиномы из k[x] , степень каждого из
которых меньше степени f.
Полином неразложим над k, если он не является разложимым над k.
5.5.1. Упражнение. Пусть f -- неразложимый полином над k.
Доказать следующие утверждения:
1. af неразложим для любого
5.5.2. Теорема. Пусть f -- ненулевой полином из k[x].
1. Существуют такие неразложимые полиномы
Доказательство. 1. Утверждение очевидно для полиномов нулевой степени
(в этом случае s=0) и неразложимых полиномов (в этом случае s=1).
В общем случае
утверждение тривиально доказывается индукцией по степени f.
2. Пусть
5.6. Корни и значения.
Пусть
5.6.1. Упражнение. Если
h=f+g, u=fg, то
h(b)=f(b)+g(b),u(b)=f(b)g(b)
для любого элемента
5.6.2. Теорема Безу. Значение полинома f в точке b равно
остатку от деления f на x-b.
Элемент b из k является корнем
Доказательство. Подставив b в равенство
5.7. Производная. Кратные корни.
Производной полинома
f = a0 +a1 x+a2 x2 +...+an xn
называется полином
5.7.1. Упражнения. Доказать следующие утверждения:
1.
Элемент
5.7.2. Теорема. Пусть k -- числовое поле (то есть k --
подполе поля C).
1.Если элемент b из k является корнем кратности m для ненулевого
полинома f,
то b -- корень кратности m-1 для
Доказательство. 1. Если
f=(x-b)mh, где h не делится на x-b,
то
5.7.3. Упражнение. Для любого полинома f степени
5.7.4. Теорема. 1. Если f -- ненулевой полином степени n,
то существует не более n
корней полинома f.
2. Если f и g -- полиномы степени <n, значения которых совпадают
в n различных точках, то f=g.
3. (Интерполяционная формула Лагранжа). Пусть f -- полином степени
<n над
Доказательство. 1. Если
b1,...,br -- все различные корни f,
то
(x-bi,x-bj)=1 при
5.7.5. Теорема. Пусть k -- числовое поле.
1. Пусть
a,a1,...,an -- попарно различные элементы из
Доказательство. 1. Индукция по r. Если r=0, то в качестве h
можно взять b0/d(a). Пусть
уже найден полином g=ud, где u -- полином степени <r, обладающий
свойством
5.8. Существование корня полинома в расширении поля.
Поле K называется расширением поля k, если k -- подполе поля K,
то есть
Теорема. Пусть
Доказательство. 1. По теореме 5.5.2
5.9. Формулы Виета. Из равенства
5.10. Полиномы от нескольких неизвестных.
Пусть
x1,x2,...,xn -- неизвестные (переменные), k -- поле.
По индукции определим кольцо
k[x1,x2,...,xn]
полиномов от
x1,x2,...,xn как
k[x1,x2,...,xn-1][xn].
Каждый полином от
x1,x2,...,xn является суммой конечного числа
мономов
вида
5.10.1. Симметрические полиномы.
Подстановкой чисел 1,2,...,n называетсся любое взаимно
однозначное отображение множества
5.10.2. Примеры.
1. Полиномы
5.10.3. Теорема. Пусть
f(x1,...,xn) -- симметрический полином
над k.
1. Существует полином
g(y1,...,yn) над k, для которого
Доказательство. Пусть
5.11. Алгебраическая замкнутость C .
Поле k называется алгебраически замкнутым, если каждый
полином из k[x]
разлагается в k[x]
на линейные множители. Цель этого раздела -- доказать, что поле C
комплексных
чисел алгебраичеки замкнуто. Мы начнем это доказательство с полиномов нечетной
степени, имеющих вещественные коэффициенты.
5.11.1. Теорема. Если
Доказательство. Можно считать, что старший коэффициент f равен 1.
Пусть
f(x) = a0 +a1 x+a2 x2 +...+an-1xn-1+xn.
Обозначим
5.11.2. Теорема. Если
Доказательство. Пусть степень f равна n=2mq, где m -- целое
неотрицательное число,
q -- нечетное число.
Индукция по m. При m=0 по предыдущей теореме искомое число c
существует даже в R.
Пусть
5.11.3. Теорема. Поле C алгебраически замкнуто.
Доказательство. Достаточно показать, что любой полином f над
C ненулевой степени
имеет в C хотя бы один корень.
Пусть
5.12. Неразложимые полиномы над C и R.
5.12.1. Теорема. 1. Если f -- полином из C[x],
неразложимый над C, то степень
Доказательство. 1 следует из теоремы 5.11.3.
2. Если f(c)=0, то
5.13. Неразложимые над Q полиномы.
Следующий результат сводит вопрос о неразложимости полинома над Q
к такому
же вопросу над Z.
5.13.1. Теорема. 1. Если
Доказательство. 1. В качестве a можно взять наименьшее общее
кратное знаменателей коэффициентов f.
2. Предположим противное. Пусть полиномы f,g примитивны, но существует
простое число p,
делящее все коэффициенты fg. При этом, по условию, p не может
делить все коэффициенты ai и не может делить все bj.
Пусть s -- наименьшее
число, для которого as не делится на p, а r -- наименьшее число,
для которого br
не делится на p.
Тогда коэффициент c при xs+r в произведении fg равен
5.13.2. Теорема. Вопрос о разложимости любого данного полинома из
Q[
![]() .
1. Существуют такие
.
1. Существуют такие
![]() , что
f=hg+r и стr< стg или r=0.
2. Многочлены h и r
определяются однозначно по полиномам f
и g.
Полином h
называется (неполным) частным, а r --
остатком от деления f
на g
.
, что
f=hg+r и стr< стg или r=0.
2. Многочлены h и r
определяются однозначно по полиномам f
и g.
Полином h
называется (неполным) частным, а r --
остатком от деления f
на g
.
![]() . Положим
f1=f-(an/bm)xn-mg
. Тогда
. Положим
f1=f-(an/bm)xn-mg
. Тогда
![]() и коэффициент многочлена f1
при xn
равен 0, поэтому стf1<n
и по индукции
f1=h1g+r
, где r=0
или стr<m
. Но тогда f=hg+r
, где
h=h1+(an/bm)xn-m.
2. Пусть
hg+r=h1g+r1
, где каждый из полиномов r,r1
удовлетворяет условию б). Тогда
(h-h1)g=r1-r
. Если
и коэффициент многочлена f1
при xn
равен 0, поэтому стf1<n
и по индукции
f1=h1g+r
, где r=0
или стr<m
. Но тогда f=hg+r
, где
h=h1+(an/bm)xn-m.
2. Пусть
hg+r=h1g+r1
, где каждый из полиномов r,r1
удовлетворяет условию б). Тогда
(h-h1)g=r1-r
. Если
![]() , то
, то
![]() ,
а
ст(r1-r)<m
. Поэтому h-h1=0
, откуда r1-r=0.
Теорема доказана.
,
а
ст(r1-r)<m
. Поэтому h-h1=0
, откуда r1-r=0.
Теорема доказана.
![]() .
Скажем, что
f делит g (или
g делится на f), если найдется
.
Скажем, что
f делит g (или
g делится на f), если найдется
![]() , для которого
g=hf. Отметим, что 0 делится на любой многочлен и, если 0 делит
g, то
g=0. Если
, для которого
g=hf. Отметим, что 0 делится на любой многочлен и, если 0 делит
g, то
g=0. Если
![]() , то
g делится на f тогда и только тогда, когда
остаток от деления
g на f
равен 0.
, то
g делится на f тогда и только тогда, когда
остаток от деления
g на f
равен 0.
![]() .
5. Два полинома тогда и только тогда делятся друг на друга,
когда они отличаются множителем нулевой степени.
.
5. Два полинома тогда и только тогда делятся друг на друга,
когда они отличаются множителем нулевой степени.
![]() .
Определим полином fn, если уже определены полиномы fn-2, fn-1
и
.
Определим полином fn, если уже определены полиномы fn-2, fn-1
и
![]() ,
с помощью следующего условия (n):
,
с помощью следующего условия (n):
![]()
1. Наибольший общий делитель полиномов f1,f2 существует: им
является полином
fm, для которого fm+1=0.
2. Существуют такие полиномы u1,u2, что
![]() . Тогда fm делит
fm-1
и равенства
(m),(m-1),...,(3) последовательно показывают, что
fm делит
fm-2,fm-3,...,f1. Далее, если полином t делит
f1 и f2, то равенства
(3),(4),...,(m) показывают, что t делит
f3,f4,...,fm. Это заканчивает проверку того, что fm -- наибольший
общий делитель полиномов f1,f2.
2. С помощью равенств
(m),(m-1),...,(3) последовательно представим fm
в виде
fm=vn-2fn-2+vn-1fn-1, n=m,m-1,...,3 и тем самым получим
2. Теорема доказана.
. Тогда fm делит
fm-1
и равенства
(m),(m-1),...,(3) последовательно показывают, что
fm делит
fm-2,fm-3,...,f1. Далее, если полином t делит
f1 и f2, то равенства
(3),(4),...,(m) показывают, что t делит
f3,f4,...,fm. Это заканчивает проверку того, что fm -- наибольший
общий делитель полиномов f1,f2.
2. С помощью равенств
(m),(m-1),...,(3) последовательно представим fm
в виде
fm=vn-2fn-2+vn-1fn-1, n=m,m-1,...,3 и тем самым получим
2. Теорема доказана.
![]() существуют
полиномы u,v, для которых uf+vg=1.
существуют
полиномы u,v, для которых uf+vg=1.
![]() следует из теоремы 5.3.3.
следует из теоремы 5.3.3.
![]() . Если uf+vg=1, то (f,g) делит 1. Теорема доказана.
. Если uf+vg=1, то (f,g) делит 1. Теорема доказана.
![]() .
2. Если полином f делит произведение hg полиномов h,g и
взаимно прост с g , то f делит h.
3. Если каждый из попарно взаимно простых полиномов
gi=1, i=1,2,...,r
делит полином f,
то произведение
.
2. Если полином f делит произведение hg полиномов h,g и
взаимно прост с g , то f делит h.
3. Если каждый из попарно взаимно простых полиномов
gi=1, i=1,2,...,r
делит полином f,
то произведение
![]() делит f.
делит f.
![]() , где
, где ![]() означает некоторые полиномы. По теореме 5.4.1
(f,g1g2)=1.
2. По теореме 5.4.1 существуют полиномы u,v, что uf+vg=1.
Отсюда ufh+vgh=h и f делит каждое слагаемое
левой части последнего равенства, то есть делит правую часть.
3. Достаточно рассмотреть случай двух полиномов. Имеем: g2 делит
f=g1h1. По 2 g2 делит h1.
Теорема доказана.
означает некоторые полиномы. По теореме 5.4.1
(f,g1g2)=1.
2. По теореме 5.4.1 существуют полиномы u,v, что uf+vg=1.
Отсюда ufh+vgh=h и f делит каждое слагаемое
левой части последнего равенства, то есть делит правую часть.
3. Достаточно рассмотреть случай двух полиномов. Имеем: g2 делит
f=g1h1. По 2 g2 делит h1.
Теорема доказана.
![]() .
2. Если
.
2. Если ![]() , то либо f делит g, либо f взаимно прост с g.
3. Если g -- ненулевой полином степени, меньшей степени f, то (f,g)=1.
, то либо f делит g, либо f взаимно прост с g.
3. Если g -- ненулевой полином степени, меньшей степени f, то (f,g)=1.
![]() , каждый из
которых имеет ненулевую степень и равный единице старший коэффициент,
и такой элемент a из k, что
, каждый из
которых имеет ненулевую степень и равный единице старший коэффициент,
и такой элемент a из k, что
![]() .
2.
a,p1,...,ps с точностью до порядка однозначно определяются
полиномом f.
.
2.
a,p1,...,ps с точностью до порядка однозначно определяются
полиномом f.
![]()
где
p1,...,ps,q1,...,qr
неразложимы и с
единичными старшими коэффициентами.
Можно считать, что ![]() . Очевидно, a=b -- старший коэффициент f
и
. Очевидно, a=b -- старший коэффициент f
и
![]() , откуда
, откуда
![]() .
Применим индукцию по s. Если s=0, то r=0, иначе слева стоит
полином нулевой степени,
а справа -- степени, большей, чем 0.
Пусть s>0. Так как p1 делит
.
Применим индукцию по s. Если s=0, то r=0, иначе слева стоит
полином нулевой степени,
а справа -- степени, большей, чем 0.
Пусть s>0. Так как p1 делит
![]() , найдется j, что
, найдется j, что
![]() . Можно считать, что j=1. Так как p1,q1 неразложимы
и их старшие коэффициенты равны 1, p1=q1. Отсюда
. Можно считать, что j=1. Так как p1,q1 неразложимы
и их старшие коэффициенты равны 1, p1=q1. Отсюда
![]() и
и
![]() .
По индукционному предположению s=r
и набор
.
По индукционному предположению s=r
и набор
![]() совпадает с набором
совпадает с набором
![]() .
Теорема доказана.
.
Теорема доказана.
![]() . Значением полинома
f в точке
. Значением полинома
f в точке ![]() (или на b, или
при x=b) называется элемент
(или на b, или
при x=b) называется элемент ![]() , равный
a0 +a1 b+a2 b2 +...+an bn. Элемент b называется корнем
полинома f, если f(b)=0.
, равный
a0 +a1 b+a2 b2 +...+an bn. Элемент b называется корнем
полинома f, если f(b)=0.
![]() . Доказать.
. Доказать.
![]() делится на
x-b.
делится на
x-b.
![]()
получим требуемое.
![]() .
.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() , если
, если ![]() .
.
![]() называется корнем кратности m для ненулевого
полинома f, если f делится на (x-b)m,
но не делится на (x-b)m. Корень кратности 1 называется простым
корнем, корень кратности m>1 называется кратным корнем.
Корень кратности 0 корнем не является.
называется корнем кратности m для ненулевого
полинома f, если f делится на (x-b)m,
но не делится на (x-b)m. Корень кратности 1 называется простым
корнем, корень кратности m>1 называется кратным корнем.
Корень кратности 0 корнем не является.
![]() .
2. Любой корень ненулевого полинома f является корнем полинома
.
2. Любой корень ненулевого полинома f является корнем полинома
![]() и все корни f1
простые.
и все корни f1
простые.
![]() , где
, где
![]() .
Полином u не делится на x-b,
так как
.
Полином u не делится на x-b,
так как ![]() и h не делится на x-b.
2. Если b -- корень кратности m>0 для f, то по 1
(x-b)m-1
делит
и h не делится на x-b.
2. Если b -- корень кратности m>0 для f, то по 1
(x-b)m-1
делит
![]() , а (x-b)m не делит
, а (x-b)m не делит
![]() , поэтому
b -- простой корень f1.
Для полинома f определим f(0) как f, f(1) как
, поэтому
b -- простой корень f1.
Для полинома f определим f(0) как f, f(1) как
![]() и, вообще, f(i+1) как
и, вообще, f(i+1) как
![]() .
.
![]() над числовым
полем k и любого
элемента b из k
доказать справедливость следующей формулы Тейлора:
над числовым
полем k и любого
элемента b из k
доказать справедливость следующей формулы Тейлора:
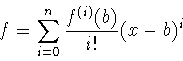
(здесь
0!=1=(x-b)0).
Указание. Заметить, что степень полинома
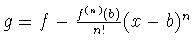 меньше n и что
f(i)(b)=g(i)(b) при i<n. Затем использовать
индукцию по n.
меньше n и что
f(i)(b)=g(i)(b) при i<n. Затем использовать
индукцию по n.
![]() -- различные элементы из k и
-- различные элементы из k и
![]() . Тогда
. Тогда
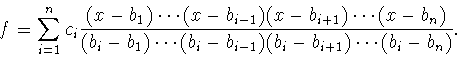
![]() и поэтому
и поэтому
![]() .
Отсюда следует, что степень f больше или равна r.
2. f-g -- полином степени <n, имеющий n различных корней,
поэтому по 1 f-g=0.
3. Обозначим правую часть формулы через g. Легко заметить, что g --
полином степени <n, значение которого в каждой точке bi совпадает
с f(bi). По 2 f=g.
.
Отсюда следует, что степень f больше или равна r.
2. f-g -- полином степени <n, имеющий n различных корней,
поэтому по 1 f-g=0.
3. Обозначим правую часть формулы через g. Легко заметить, что g --
полином степени <n, значение которого в каждой точке bi совпадает
с f(bi). По 2 f=g.
![]() -- целые неотрицательные числа.
Положим
-- целые неотрицательные числа.
Положим
![]() .
Существует полином
.
Существует полином ![]() степени
степени ![]() , для которого полином f=hd
при всех j=0,...,r обладает свойством:
f(j)(a)=bj.
2. (Интерполяционный полином Лагранжа - Сильвестра).
Пусть
a,a1,...,an --
попарно различные элементы из
, для которого полином f=hd
при всех j=0,...,r обладает свойством:
f(j)(a)=bj.
2. (Интерполяционный полином Лагранжа - Сильвестра).
Пусть
a,a1,...,an --
попарно различные элементы из
![]() .
Существует однозначно определенный полином f над k степени
.
Существует однозначно определенный полином f над k степени
![]() , для которого
, для которого
![]()
.
![]()
Тогда полином
f=(u+cr(x-a)r)d =g+cr(x-a)rd
также обладает этим свойством при любом ![]() . Кроме того,
. Кроме того,
где ![]() , и поэтому
f(r)(a)=(ud)(r)(a)+c!d(a).
Таким образом,
достаточно взять
cr=(br-(ud)(r)(a))/r!d(a).
2. По пункту 1. можно для любого i=1,...,n найти такой полином hi
степени
, и поэтому
f(r)(a)=(ud)(r)(a)+c!d(a).
Таким образом,
достаточно взять
cr=(br-(ud)(r)(a))/r!d(a).
2. По пункту 1. можно для любого i=1,...,n найти такой полином hi
степени ![]() , что полином
, что полином
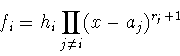
обладает свойством
![]()
![]()
Кроме того, очевидно, что степень fi меньше
![]() .
Поэтому
f=f1+...+fn --
искомый полином.
Если g -- еще один полином с теми же свойствами, то
(f-g)(s)(ai)=0 для всех i=1,...,n и всех
s=0,...,ri, поэтому
f-g по теореме 5.7.2 делится на
.
Поэтому
f=f1+...+fn --
искомый полином.
Если g -- еще один полином с теми же свойствами, то
(f-g)(s)(ai)=0 для всех i=1,...,n и всех
s=0,...,ri, поэтому
f-g по теореме 5.7.2 делится на
![]() ,
а поскольку его степень меньше
,
а поскольку его степень меньше
![]() , то f-g=0.
Теорема доказана.
, то f-g=0.
Теорема доказана.
![]() и ограничение
каждой операции поля K на множестве k совпадает с соответствующей
операцией поля k.
В частности, если K -- расширение k, то k[x] -- подкольцо в K[x].
и ограничение
каждой операции поля K на множестве k совпадает с соответствующей
операцией поля k.
В частности, если K -- расширение k, то k[x] -- подкольцо в K[x].
![]() и степень f больше нуля.
1. Существует расширение K поля k и элемент b из K,
для которого f(b)=0.
2. Существует расширение K поля k и элементы
и степень f больше нуля.
1. Существует расширение K поля k и элемент b из K,
для которого f(b)=0.
2. Существует расширение K поля k и элементы
![]() , что
, что
![]()
где a -- старший коэффициент f.
![]() , где p1 --
неразложимый полином степени >0
со старшим коэффициентом, равным 1. Поскольку любой корень p1
является корнем f, достаточно
доказать теорему для случая, когда f=p1, то есть когда f --
неразложимый полином
со старшим коэффициентом, равным 1.
Пусть
f(x) = a0 +a1 x+a2 x2 +...+xn.
Положим
, где p1 --
неразложимый полином степени >0
со старшим коэффициентом, равным 1. Поскольку любой корень p1
является корнем f, достаточно
доказать теорему для случая, когда f=p1, то есть когда f --
неразложимый полином
со старшим коэффициентом, равным 1.
Пусть
f(x) = a0 +a1 x+a2 x2 +...+xn.
Положим
![]() . В качестве операции
сложения возьмем обычную операцию +
сложения полиномов, а операцию умножения
. В качестве операции
сложения возьмем обычную операцию +
сложения полиномов, а операцию умножения ![]() определим следующим правилом:
определим следующим правилом:
![]() есть остаток от деления h(y)g(y) на f(y).
Непосредственно проверяется, что операции сложения и умножения в K
коммутативны
и ассоциативны и что справедлив закон дистрибутивности. Нуль 0 и
единица 1 поля k
являются, соответственноб нулем и единицей поля K. Кроме того, для любого
h из K существует противоположный элемент -h.
Осталось проверить существование обратного
элемента для любого ненулевого элемента h из k. Поскоьку степень h
меньше n и f
неразложим, из упражнения 5.5.1 (3) следует, что
((h(y),f(y))=1
и, значит, по теореме 5.3.3 и упражнению 5.3.4 существуют полиномы
есть остаток от деления h(y)g(y) на f(y).
Непосредственно проверяется, что операции сложения и умножения в K
коммутативны
и ассоциативны и что справедлив закон дистрибутивности. Нуль 0 и
единица 1 поля k
являются, соответственноб нулем и единицей поля K. Кроме того, для любого
h из K существует противоположный элемент -h.
Осталось проверить существование обратного
элемента для любого ненулевого элемента h из k. Поскоьку степень h
меньше n и f
неразложим, из упражнения 5.5.1 (3) следует, что
((h(y),f(y))=1
и, значит, по теореме 5.3.3 и упражнению 5.3.4 существуют полиномы
![]() , что степень u меньше n и hu=-fv+1. Это означает, что
, что степень u меньше n и hu=-fv+1. Это означает, что
![]() и u -- обратный элемент к h в k.
Нулевой полином и полиномы нулевой степени из K являются элементами из
k, поэтому K -- расширение k.
Положим
и u -- обратный элемент к h в k.
Нулевой полином и полиномы нулевой степени из K являются элементами из
k, поэтому K -- расширение k.
Положим ![]() . Тогда
. Тогда
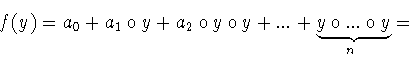
![]()
поскольку
-(a0 +a1 y+a2 y2 +...+an-1yn-1) -- остаток от деления
yn на
=a0 +a1 y+a2 y2 +...+an-1yn-1+yn.
2. Индукция по степени f. По 1 существует элемент b1 в некотором
расширении K1 поля k, для которого
f=f1(x-b1), где
![]() .
По индукции существует расширение K поля K1,
для которого
.
По индукции существует расширение K поля K1,
для которого
![]() , где
, где
![]() --
старший коэффициент f1 = старший коэффициент f. Тогда K --
расширение
--
старший коэффициент f1 = старший коэффициент f. Тогда K --
расширение
![]() и
и
![]() . Теорема доказана.
Поле K из пункта 2 теоремы называется полем разложения полинома
f над k.
. Теорема доказана.
Поле K из пункта 2 теоремы называется полем разложения полинома
f над k.
![]()
где ![]() и
b1,...,bn --
все корни f с учетом их кратностей,
вытекают равенства
и
b1,...,bn --
все корни f с учетом их кратностей,
вытекают равенства
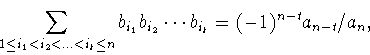
которые называются формулами Виета для полинома f.
![]() , где
, где
![]() -- целые неотрицательные числа. Строка
(m1,...,mn) называется
степенью монома
-- целые неотрицательные числа. Строка
(m1,...,mn) называется
степенью монома
![]() .
Упорядочим степени по правилу:
(m1,...,mn)>(p1,...,pn) , если
m1>p1 или если найдется натуральное число s<n,
что
m1=p1,...,ms=ps,ms+1>ps+1.
Ясно, что из двух разных степеней одна больше другой и отношение ">" для
степеней транзитивно.
Старшим мономом полинома назовем его моном наибольшей степени.
Степенью
полинома назовем степень его старшего монома.
Из определения легко следует, что старший моном произведения полиномов
равен произведению старших мономов сомножителей.
.
Упорядочим степени по правилу:
(m1,...,mn)>(p1,...,pn) , если
m1>p1 или если найдется натуральное число s<n,
что
m1=p1,...,ms=ps,ms+1>ps+1.
Ясно, что из двух разных степеней одна больше другой и отношение ">" для
степеней транзитивно.
Старшим мономом полинома назовем его моном наибольшей степени.
Степенью
полинома назовем степень его старшего монома.
Из определения легко следует, что старший моном произведения полиномов
равен произведению старших мономов сомножителей.
![]() на себя, то есть
функция
на себя, то есть
функция ![]() , заданная на M и
принимающая значения в M, для которой
, заданная на M и
принимающая значения в M, для которой
![]() ,
если
,
если ![]() . Полином
f(x1,...,xn) называется симметрическим,
если
. Полином
f(x1,...,xn) называется симметрическим,
если
![]() для любой
подстановки
для любой
подстановки ![]() .
.
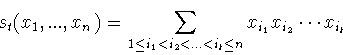
являются симметрическими.
Они называются основными (или
элементарными) симметрическими полиномами от
x1,...,xn.
2. Полином
x1t+...+xntявляется симметрическим при любом натуральном t.
3. Полином
3x1x2+3x1x3 не является симметрическим.
Поскольку сумма и произведение симметрических полиномов -- симметрические
полиномы, множество симметрических полиномов от n переменных является
кольцом --
подкольцом кольца всех полиномов от n переменных.
Если
![]() , а
p1,...,pm -- симметрические
полиномы от
x1,...,xn, то
, а
p1,...,pm -- симметрические
полиномы от
x1,...,xn, то
-- симметрический полином от
x1,...,xn.
где
s1,...,sn -- основные симметрические
полиномы.
2. Если h -- полином степени n из k[x] и
b1,...,bn -
все его корни
(существующие в некотором расширении поля k), то
![]() .
.
![]() -- старший
моном f. Заметим, что
-- старший
моном f. Заметим, что
![]() . Действительно, если
mi<mi+1 для некоторого i, то f содержит моном
. Действительно, если
mi<mi+1 для некоторого i, то f содержит моном
![]() (получающийся из
старшего монома f
подстанокой
(получающийся из
старшего монома f
подстанокой ![]() :
:
![]() для
для
![]() ), степень которого больше, чем
(m1,...,mn). Пусть
), степень которого больше, чем
(m1,...,mn). Пусть
![]() , где
s1,...,sn -- основные
симметрические полиномы от
x1,...,xn. Тогда старший моном полинома u
равен старшему
моному полинома f и полином f1=f-u является симметрическим полиномом,
степень которого меньше степени f.
Поскольку степень
(l1,...,ln) произвольного симметрического полинома
обладает свойством
, где
s1,...,sn -- основные
симметрические полиномы от
x1,...,xn. Тогда старший моном полинома u
равен старшему
моному полинома f и полином f1=f-u является симметрическим полиномом,
степень которого меньше степени f.
Поскольку степень
(l1,...,ln) произвольного симметрического полинома
обладает свойством
![]() , существует
только конечное число степеней симметрических полиномов, меньших
(m1,...,mn), поэтому
можно применить индукцию по степени и считать, что для f1 существует полином
, существует
только конечное число степеней симметрических полиномов, меньших
(m1,...,mn), поэтому
можно применить индукцию по степени и считать, что для f1 существует полином
![]() , для которого
f1=g1(s1,...,sn).
Отсюда искомый полином g равен
, для которого
f1=g1(s1,...,sn).
Отсюда искомый полином g равен
![]()
2. По 1
где
![]() , поэтому из формул Виета 5.9 следует, что
, поэтому из формул Виета 5.9 следует, что
где
a0,...,an -- коэффициенты
полинома h.
Так как все ai и коэффициенты полинома g лежат в k, то
![]() . Теорема доказана.
. Теорема доказана.
![]() R[x]
и степень f нечетна,
то существует
R[x]
и степень f нечетна,
то существует ![]() R, что f(c)=0.
R, что f(c)=0.
![]() через A,
через A,
![]() -- через B.
Если
-- через B.
Если ![]() , то
, то
![]() . Это неравенство показывает, что
. Это неравенство показывает, что
![]() . Поскольку f(x) -- непрерывная функция
вещественного аргумента, на отрезке (-B,B) существует корень c полинома
f. Теорема доказана.
. Поскольку f(x) -- непрерывная функция
вещественного аргумента, на отрезке (-B,B) существует корень c полинома
f. Теорема доказана.
![]() R[x]
и степень f больше нуля,
то существует
R[x]
и степень f больше нуля,
то существует ![]() C, что f(c)=0.
C, что f(c)=0.
![]() и теорема верна для всех полиномов над R,
степень которых не делится на 2m.
Пусть K -- поле разложения f над C и
b1,...,bn --
корни f в K. Выберем произвольное вещественное
число r и для каждой пары
(bi,bj)i<j различных корней f рассмотрим
элемент
cij=bibj+r(bi+bj) из K. Положим
и теорема верна для всех полиномов над R,
степень которых не делится на 2m.
Пусть K -- поле разложения f над C и
b1,...,bn --
корни f в K. Выберем произвольное вещественное
число r и для каждой пары
(bi,bj)i<j различных корней f рассмотрим
элемент
cij=bibj+r(bi+bj) из K. Положим
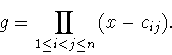
Степень полинома g равна
t=n(n-1)/2=2m-1p, где p=q(n-1) нечетно.
Коэффициенты полинома g по формулам Виета -- значения
симметрических полиномов от t переменных над R при подстановке
в них элементов cij, и поскольку любая перестановка
b1,...,bn
приводит лишь
к перестановке элементов cij, эти коэффициенты -- значения симметрических
полиномов над R от
x1,...,xn при
![]() .
По теореме 5.10.3 коэффициенты полинома g лежат в R. По
предположению индукции
.
По теореме 5.10.3 коэффициенты полинома g лежат в R. По
предположению индукции ![]() C для некоторой пары (i,j).
Поскольку для выбора числа r
имеется бесконечно много возможностей, найдутся два таких различных
вещественных числа r,s,
что для одной и той же пары (i,j) элементы
C для некоторой пары (i,j).
Поскольку для выбора числа r
имеется бесконечно много возможностей, найдутся два таких различных
вещественных числа r,s,
что для одной и той же пары (i,j) элементы
![]() одновременно лежат в C.
Но тогда
одновременно лежат в C.
Но тогда
![]() C , откуда
C , откуда
![]() C. Теорема доказана.
C. Теорема доказана.
![]() , где
, где
![]()
Тогда ![]() R[x]
и
по теореме 5.11.2
существует
R[x]
и
по теореме 5.11.2
существует ![]() C, для которого
C, для которого
![]() .
Если
.
Если
![]() , то
, то
![]() и, значит,
и, значит,
![]() .
Теорема доказана.
.
Теорема доказана.
![]() .
2. Пусть c -- комплексный корень полинома
.
2. Пусть c -- комплексный корень полинома ![]() R.
Тогда число, комплексно сопряженное с c, также является корнем f.
3. Если f -- полином из R[x], неразложимый над
R, то степень
R.
Тогда число, комплексно сопряженное с c, также является корнем f.
3. Если f -- полином из R[x], неразложимый над
R, то степень ![]() .
.
![]() .
3. Пусть степень f больше 2. По теореме 5.11.2 существует
.
3. Пусть степень f больше 2. По теореме 5.11.2 существует ![]() C, что f(c)=0.
Если
C, что f(c)=0.
Если ![]() R, то
f=f1(x-c) и f
разложим над R.
Если
R, то
f=f1(x-c) и f
разложим над R.
Если ![]() R, то
R, то
![]() и
и
![]() по 2. Поскольку
по 2. Поскольку
![]() ,
полином f делится на
,
полином f делится на
![]() R
и, следовательно, f разложим
над R. Теорема доказана.
R
и, следовательно, f разложим
над R. Теорема доказана.
![]() Q[x], то существует
натуральное число a,
что
Q[x], то существует
натуральное число a,
что ![]() Z[x].
2. (Лемма Гаусса). Назовем полином с целыми коэффициентами примитивным,
если наибольший общий делитель его коэффициентов равен 1.
Произведение любых двух примитивных полиномов -- примитивный полином.
3. Полином с целыми коэффициентами, неразложимый над Z,
неразложим над Q.
Z[x].
2. (Лемма Гаусса). Назовем полином с целыми коэффициентами примитивным,
если наибольший общий делитель его коэффициентов равен 1.
Произведение любых двух примитивных полиномов -- примитивный полином.
3. Полином с целыми коэффициентами, неразложимый над Z,
неразложим над Q.
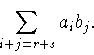
При i<s слагаемое aibj этой суммы делится на p, поскольку ai
делится на p; если i>s, то j<r и aibj делится на p, поскольку
bj делится на p; если i=s, то j=r и aibj не делится на p.
Поэтому c не делится на p. Противоречие.
3. Пусть ![]() Z[x] и неразложим над Z. Предположим,
f=gh, где
Z[x] и неразложим над Z. Предположим,
f=gh, где
![]() Q[x] и степени g и h меньше степени f. Пусть d
-- наибольший общий делитель коэффициентов f. Тогда f=dp, где полином
p примитивен. Теперь,
используя 1, легко получить равенство qp=uv, где q -- рациональное число,
u,v -- примитивные
полиномы, являющиеся скалярными кратными полиномов g,h. Так как
Q[x] и степени g и h меньше степени f. Пусть d
-- наибольший общий делитель коэффициентов f. Тогда f=dp, где полином
p примитивен. Теперь,
используя 1, легко получить равенство qp=uv, где q -- рациональное число,
u,v -- примитивные
полиномы, являющиеся скалярными кратными полиномов g,h. Так как ![]() Z[x] и p -- примитивный полином, то q -- целое число.
Поскольку полиномы u,v примитивны, то
Z[x] и p -- примитивный полином, то q -- целое число.
Поскольку полиномы u,v примитивны, то ![]() и
и
![]() --
произведение полиномов из Z[x], степени которых
меньше степени f. Теорема доказана.
--
произведение полиномов из Z[x], степени которых
меньше степени f. Теорема доказана.