6.1. Определение. Линейное отображение V в V называется линейным преобразованием векторного пространства V. Таким образом,
На протяжении всей главы V будет означать векторное пространство
размерности n над полем k.
6.1. Определение. Линейное отображение V в V называется
линейным преобразованием векторного пространства V. Таким образом,
![]() -- линейное преобразование V, если
-- линейное преобразование V, если ![]() -- функция,
заданная на V со значениями в V и удовлетворяющая следующим двум
условиям:
-- функция,
заданная на V со значениями в V и удовлетворяющая следующим двум
условиям:
![]() при
всех
при
всех
![]() .
Эти два условия можно заменить на одно:
.
Эти два условия можно заменить на одно:
![]() при всех
при всех
![]() N.
Совокупность всех линейных преобразований пространства V
обозначается
через
N.
Совокупность всех линейных преобразований пространства V
обозначается
через
![]() .
Ясно, что
.
Ясно, что
![]() .
.
6.1.2. Примеры - упражнения. Показать, что ![]() - линейное
преобразования соответствующего векторного пространства.
1. V - пространство векторов вещественной плоскости с
началом в точке O,
а)
- линейное
преобразования соответствующего векторного пространства.
1. V - пространство векторов вещественной плоскости с
началом в точке O,
а) ![]() - симметрия относительно точки O,
б)
- симметрия относительно точки O,
б) ![]() - симметрия относительно прямой, проходящей через
O,
в)
- симметрия относительно прямой, проходящей через
O,
в) ![]() - поворот плоскости вокруг O на данной угол.
2.
- поворот плоскости вокруг O на данной угол.
2. ![]() - дифференцирование в пространстве полиномов k[x]:
- дифференцирование в пространстве полиномов k[x]:
![]() для
для ![]() .
3. Пусть
.
3. Пусть
![]() ,
,
![]() - умножение строки из пространства
kn на A:
- умножение строки из пространства
kn на A:
Если ![]() ,
,
![]() и
и
![]() ,
то u называется образом v под действием
,
то u называется образом v под действием ![]() ,
а v
-- прообразом u. Если
,
а v
-- прообразом u. Если
![]() ,
то множество
,
то множество
![]() называется образом A под
действием
называется образом A под
действием ![]() .
.
6.1.3. Матрица линейного преобразования.
Пусть ![]() - база
V,
- база
V,
![]() .
Матрицей [
.
Матрицей [![]() ]
=
]
=
![]() преобразования
преобразования ![]() в базе
в базе ![]() называется
матрица линейного отображения
называется
матрица линейного отображения
![]() относительно пары баз
относительно пары баз
![]() .
Таким образом, если
.
Таким образом, если
![]() и
и
![\begin{displaymath}[\varphi ]= \left[ \begin{array}{lcr}
a_{11}, & ... & a_{1n}...
...... & ... & ... \\
a_{n1}, & ... & a_{nn} \end{array} \right]\end{displaymath}](img33000.gif)
![$\left[ \begin{array}{l}
u_1\\ u_2 \\ ...\\ u_n \end{array} \right]$](img34000.gif) через
через ![$\left[ \begin{array}{l}
u_1\varphi\\ u_2\varphi \\ ...\\ u_n\varphi \end{array} \right]$](img36000.gif) -- через
-- через
6.1.4. Координаты образа вектора.
Пусть ![]() - база
V,
- база
V,
![]() - матрица
- матрица ![]() в базе
в базе
![]() .
Если
.
Если ![]() ,
то, как и раньше, через [a] обозначим строку
координат
вектора a в базе
,
то, как и раньше, через [a] обозначим строку
координат
вектора a в базе ![]() .
Напомним, что
.
Напомним, что
![]() .
.
Теорема. Если ![]() , то
, то
![]() .
.
Доказательство. Имеет место цепочка равенств
6.1.5. Связь между
![]() и Mn(k).
и Mn(k).
Для
![]() и
и
![]() определим
отображения
определим
отображения
![]() и
и
![]() пространства V
в V равенствами
пространства V
в V равенствами
Теорема. Пусть ![]() - база
V. Тогда соответствие
- база
V. Тогда соответствие
![]() (линейному преобразованию
(линейному преобразованию ![]() сопоставляется его матрица в базе
сопоставляется его матрица в базе
![]() )
дает взаимно однозначное отображение множества
)
дает взаимно однозначное отображение множества
![]() на Mn(k).
Если
на Mn(k).
Если
![]() , то
, то
![]() и имеют место равенства
и имеют место равенства
6.1.6. Матрицы линейного преобразования в разных базах.
Пусть
![]() -- две базы
-- две базы
![]() --
матрица
перехода от
--
матрица
перехода от ![]() к
к ![]() .
Это означает (см. 2.4.9), что
.
Это означает (см. 2.4.9), что
Теорема. Матрицы одного и того же линейного преобразования
пространства V в двух базах подобны над k. Подобие осуществляет
матрица перехода от одной базы к другой.
Упражнение. Докажите обратное утверждение: пусть X и Y --
две матрицы из Mn(k), сопряженные над k. Тогда X и Y -- матрицы
одного и того же линейного преобразования в подходящих базах.
Указание. Если
![]() -- база
-- база ![]() --
невырожденная матрица из
Mn(k), то элементы столбца
--
невырожденная матрица из
Mn(k), то элементы столбца ![]() образуют базу V.
образуют базу V.
6.1.7. Образ и ядро, ранг и дефект.
Если
![]() ,
то множество
,
то множество
![]() называется образом
называется образом ![]() ,
а
множество
,
а
множество
![]() называется ядром
называется ядром ![]() .
.
Теорема. 1. ![]() и
и
![]() --
подпространства пространства V.
Размерность
--
подпространства пространства V.
Размерность ![]() называется рангом, а размерность
называется рангом, а размерность
![]() -- дефектом
-- дефектом ![]() .
2. Сумма ранга и дефекта линейного преобразования равна
размерности пространства.
3. Ранг
.
2. Сумма ранга и дефекта линейного преобразования равна
размерности пространства.
3. Ранг ![]() равен рангу
равен рангу
![]() (в любой базе).
(в любой базе).
Доказательство. Эта теорема - частный случай теоремы 2.5.7.
6.1.8. Невырожденное преобразование.
Теорема-определение.
Пусть
![]() . Следующие свойства
. Следующие свойства ![]() эквивалентны:
1.
эквивалентны:
1.
![]() .
2.
.
2.
![]() .
3. Образ произвольной базы -- база.
4. Матрица
.
3. Образ произвольной базы -- база.
4. Матрица ![]() невырождена (в любой базе).
5. Существует обратное преобразование
невырождена (в любой базе).
5. Существует обратное преобразование
![]() и
оно линейно.
Если
и
оно линейно.
Если ![]() обладает одним из этих свойств, то
обладает одним из этих свойств, то ![]() называется
невырожденным линейным преобразованием.
называется
невырожденным линейным преобразованием.
Доказательство. 1. ![]() 2. поскольку
размерность V равна
сумме ранга и дефекта преобразования
2. поскольку
размерность V равна
сумме ранга и дефекта преобразования ![]() .
1.
.
1.
![]() 3. Пусть
3. Пусть
![]() -- база V.
Если
-- база V.
Если
![]() линейно зависимы, то существует
ненулевая строка
(a1,...an), для которой
линейно зависимы, то существует
ненулевая строка
(a1,...an), для которой
![]() ,
поэтому
,
поэтому
![]() .
Противоречие. Поскольку n линейно независимых векторов из V
составляют базу, то
.
Противоречие. Поскольку n линейно независимых векторов из V
составляют базу, то
![]() -- база.
3.
-- база.
3.
![]() 4. Матрица
4. Матрица ![]() в базе
в базе ![]() --
матрица перехода от
--
матрица перехода от ![]() к
базе
к
базе
![]() (см. 6.1.6). Поэтому
(см. 6.1.6). Поэтому
![]() невырождена.
4.
невырождена.
4.
![]() 5. Пусть
5. Пусть ![]() -- линейное преобразование,
для которого
-- линейное преобразование,
для которого
![]() .
Тогда
.
Тогда
![]() и,
значит,
и,
значит,
![]() -- тождественное
преобразование.
5.
-- тождественное
преобразование.
5.
![]() 1. Пусть
1. Пусть
![]() .
Тогда
.
Тогда
![]() ,
откуда
,
откуда
![]() и
и
![]() .
.
6.1.9. Инвариантное подпространство и ограничение.
Пусть
![]() .
Подпространство U пространства V называется
.
Подпространство U пространства V называется![]() -инвариантным подпространством или подпространством,
инвариантным относительно
-инвариантным подпространством или подпространством,
инвариантным относительно ![]() ,
если
,
если
![]() .
Если подпространство U инвариантного относительно
.
Если подпространство U инвариантного относительно ![]() ,
то
отображение
,
то
отображение
![]() ,
определенное равенством
,
определенное равенством
![]() для всех
для всех ![]() является линейным преобразованием пространства U. Оно называется
ограничением
является линейным преобразованием пространства U. Оно называется
ограничением ![]() на Uи обозначается через
на Uи обозначается через
![]() .
.
Теорема. 1. Пусть подпространство U инвариантно
относительно
![]() -- база
-- база
![]() -- согласованная с ней
база V. Тогда
-- согласованная с ней
база V. Тогда
![\begin{displaymath}[\varphi ]=
\left[
\begin{array}{lr}
[\varphi _{\mid U}] & O\\ \ast & \ast
\end{array}\right].\end{displaymath}](img10100.gif)
![\begin{displaymath}[\varphi ]=
\left[
\begin{array}{lcr}
[\varphi _{{\mid U}_...
.... & ...\\ O & ... & [\varphi _{{\mid U}_s}]
\end{array}\right]\end{displaymath}](img10900.gif)
Доказательство -- непосредственное применение определения
![]() и
и
![]() .
.
6.1.10. Одномерное инвариантное подпространство. Собственные
векторы и собственные значения. Характеристический полином и
характеристические корни.
Пусть
![]() -- подпространство размерности 1,
инвариантное относительно
-- подпространство размерности 1,
инвариантное относительно ![]() .
Тогда U=ku, где u -- ненулевой
вектор из V и
.
Тогда U=ku, где u -- ненулевой
вектор из V и
![]() ,
где
,
где ![]() .
Наоборот, если
u - ненулевой
вектор из V и
.
Наоборот, если
u - ненулевой
вектор из V и
![]() ,
где
,
где ![]() ,
то U=ku -- одномерное
,
то U=ku -- одномерное
![]() -инвариантное подпространство.
Ненулевой вектор u
вектор из V, для которого
-инвариантное подпространство.
Ненулевой вектор u
вектор из V, для которого
![]() ,
где
,
где ![]() ,
называется
собственным вектором преобразования
,
называется
собственным вектором преобразования ![]() , соответствующим
собственному значению l.
, соответствующим
собственному значению l.
Теорема. Пусть
![]() .
1. Полином
.
1. Полином
Доказательство. 1. Пусть A и B -- матрицы преобразования
![]() в двух базах. По 6.1.6
A=C-1BC для некоторой невырожденной
матрицы C. Поэтому
в двух базах. По 6.1.6
A=C-1BC для некоторой невырожденной
матрицы C. Поэтому
![\begin{displaymath}[\varphi ]=\left[\begin{array}{lccr} l & 0 & ... & 0 \\
* & * & * & * \end{array}\right]\end{displaymath}](img11900.gif)
Если
![]() ,
то
,
то
![]() называется
характеристическим полиномом матрицы A.
называется
характеристическим полиномом матрицы A.
Упражнения. 1. Для матрицы
![]() -- полином
степени n над k. Доказать.
2. Доказать, что
-- полином
степени n над k. Доказать.
2. Доказать, что
![]() тогда и только тогда подобна
над k диагональной матрице, когда существует база V, состоящая из
собственных векторов
тогда и только тогда подобна
над k диагональной матрице, когда существует база V, состоящая из
собственных векторов ![]() .
3. Проверить, что
.
3. Проверить, что
![$\left[\begin{array}{lr} 1 & 1 \\ 0 & 1
\end{array}\right]$](img12700.gif) не подобна диагональной матрице.
4. Проверить, что для дифференцирования
не подобна диагональной матрице.
4. Проверить, что для дифференцирования ![]() пространства
полиномов степени
пространства
полиномов степени ![]() при
при ![]() нет базы, состоящей из собственных
векторов
нет базы, состоящей из собственных
векторов ![]() .
.
6.1.11. Значения полинома от матрицы и от линейного
преобразования. Теорема Кэли - Гамильтона
Пусть
![]() .
Положим
.
Положим
![]() ,
где
,
где
![]() (i сомножителей).
(i сомножителей).
Упражнение. Пусть
![]() .
Доказать, что
.
Доказать, что
Теорема Кэли - Гамильтона. 1. Пусть
![]() --
характеристический полином A. Тогда f(A) -- нулевая матрица
("Вольная" формулировка: матрица -- корень своего характеристического
полинома).
2. Пусть
--
характеристический полином A. Тогда f(A) -- нулевая матрица
("Вольная" формулировка: матрица -- корень своего характеристического
полинома).
2. Пусть
![]() -- характеристический
полином
-- характеристический
полином ![]() . Тогда
. Тогда
![]() -- нулевое преобразование (Линейное преобразование -- корень своего
характеристического полинома).
-- нулевое преобразование (Линейное преобразование -- корень своего
характеристического полинома).
Доказательство. 1. Пусть
f(x)=a0+a1x+...+anxn --
характеристический полином матрицы A. Пусть bij -- алгебраическое
дополнение к элементу
с номером ji в матрице A-xE. Очевидно,
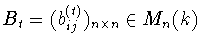 .
По теореме 3.3
.
По теореме 3.3