§4. Теория сравнений
Пункт 23. Дальнейшие свойства символа Лежандра. Закон взаимности Гаусса.
Какая песня без баяна, какой курс теории чисел без удивительного закона взаимности Гаусса! В этом пункте я расскажу об этом законе, ибо без него традиционный курс теории чисел как дом без дверей, машина без руля или (страшно подумать!) дизентерия без самого главного симптома.
Историческое отступление про Гаусса.
Карл Фридрих Гаусс (1777 – 1855) – величественная фигура математики рубежа восемнадцатого - девятнадцатого столетий. Он родился в немецком городке Брауншвейге, был сыном поденщика. Математические способности Гаусса проявились очень рано, а, согласно его дневникам, в 17 лет Карл Фридрих уже начал делать выдающиеся математические открытия. Дебютом Гаусса явилось доказательство возможности построения правильного семнадцатиугольника циркулем и линейкой (Записью об этом открывается дневник Гаусса – удивительная летопись гениальных открытий. Запись датирована 30 марта 1796 года). Отдадим должное герцогу Брауншвейгскому, который обратил внимание на вундеркинда Гаусса и позаботился о его обучении. В 1795 – 1798 годах юный гений учился в Геттингенском университете, в 1799 году он получил степень доктора, а с 1807 года до самой смерти он спокойно работал в качестве директора астрономической обсерватории и профессора математики Геттингенского университета. Как и его великие современники Кант, Гете, Бетховен и Гегель, Гаусс не вмешивался в яростные политические события той эпохи (“Буря и натиск”, наполеоновские войны, Великая Французская революция и т.п.), но в области математики он очень ярко выразил новые идеи своего века.
Обладая феноменальными вычислительными способностями, Гаусс составил огромные таблицы простых чисел (ему были известны все простые числа, меньшие пяти миллионов) и самостоятельно, путем внимательного их разглядывания, он открыл квадратичный закон взаимности (до Гаусса этот закон впервые подметил Эйлер, но не смог его доказать): если р и q – два нечетных простых числа, то
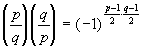
Сам Гаусс не пользовался для записи этого закона символом Лежандра, хотя знал этот формализм (Лежандр был на 20 лет старше Гаусса), да и выражения “квадратичная взаимность” у Гаусса нет (его потом придумал Дирихле). В знаменитой книге Гаусса “Арифметические исследования”, которая считается родоначальницей современной теории чисел (издана в Лейпциге, в 1801 году), отмечается, что сам закон квадратичной взаимности впервые сформулировал Эйлер, подробно обсуждал Лежандр, но до 1801 года не было опубликовано ни одного строгого доказательства этого закона. Свое первое доказательство закона взаимности Гаусс (а он, впоследствии, придумал их аж шесть штук!) получил в 1796 году * ), в девятнадцатилетнем возрасте, ценой невероятного напряжения. На отыскание первого доказательства у Гаусса ушло более года работы, которая, по меткому выражению Кроннекера, явилась серьезной “пробой гауссовского гения”. Столь выдающийся результат Гаусса был назван современниками (конечно, не всеми, а только смыслящими в математике) “золотая теорема” (“theorema aurum”). Давайте и мы познакомимся с этой золотой теоремой.
Нам понадобится несколько дополнительных свойств символа Лежандра ( a / p ), которые я сформулирую в виде лемм.
Пусть р – нечетное простое число, S ={1,2,…,( p -1)/2} - множество всех положительных чисел из приведенной системы вычетов по модулю р .
Рассмотрим сравнение a Ч s є e s r s (mod p ), где а - числитель исследуемого символа Лежандра, s О S , e s r s - абсолютно наименьший вычет числа as по модулю р (т.е. вычет, абсолютная величина которого наименьшая), r s - абсолютная величина этого вычета, а e s , стало быть, его знак. Таким образом, r s О S , а e s = ± 1.
Лемма 1 (Гаусс).
.
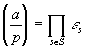Доказательство. Рассмотрим сравнения
(*)
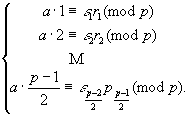Множество чисел
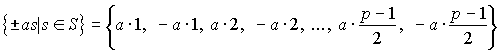
является приведенной системой вычетов по модулю р (Если забыл, см. пункт 17, лемма 2, если забыла, см. там же.). Их абсолютно наименьшие вычеты соответственно суть
,
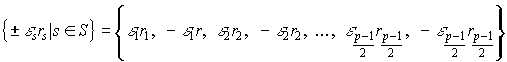положительные же из них, т.е. r 1 , r 2 ,…, r ( p -1)/2 , совпадают с числами 1,2,…,( p -1)/2, т.е. образуют множество S . Перемножим теперь почленно сравнения (*) и сократим произведение на
.
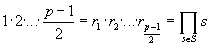Получим:
a ( p -1)/2 є e 1 e 2 … e ( p -1)/2 (mod p )
Согласно критерию Эйлера из предыдущего пункта,
a
(
p
-1)/2
є
(
a/p
)(mod
p
) т.е.
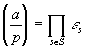, что и требовалось.
Ё
Лемма 2.
При нечетном
а
,
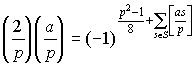, где [
as/p
] - целая часть числа
as/p
.
Доказательство. Имеем:
,
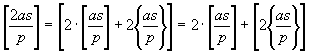что будет четным или нечетным, в зависимости от того, будет ли наименьший неотрицательный вычет числа as меньше или больше числа p /2, т.е. будет ли e s =1 или e s =-1. Отсюда, очевидно,
,
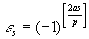поэтому, в силу леммы Гаусса,
.
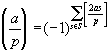Преобразуем это равенство (помним, что а + р – четное, а квадратичный множитель из числителя символа Лежандра можно отбрасывать):
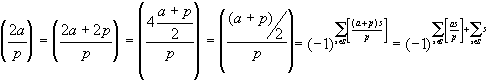
Поскольку(2
a
/
p
)=(2/
p
)(
a
/
p
), а
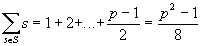, то лемма 2 доказана.
Ё
Лемма 3.
.
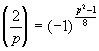Доказательство. Непосредственно следует из леммы 2 при а =1.
Ё
Ни у кого не должно возникать недоумения по поводу возможности деления числа p 2 -1=( p -1)( p +1) на 8 нацело, т.к. из двух последовательных четных чисел одно обязательно делится на 4. Кроме того, простое число р можно представить в виде p= 8 n + k , где k – одно из чисел 1, 3, 5, 7. Так как число
| (8 n + k ) 2 -1 | k 2 -1 | |
|
|
=8 n +2 +2 nk + |
|
| 8 | 8 |
будет четным при k =1 и k =7 , то 2 будет квадратичным вычетом по модулю р , если р вида 8 n +1 или 8 n +7 . Если же р вида 8 n +3 или 8 n +5 , то 2 будет квадратичным невычетом.
Теорема (Закон взаимности квадратичных вычетов). Если p и q - нечетные простые числа, то
.
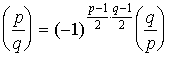Другими словами, если хоть одно из чисел p или q вида 4 n +1, то р квадрат по модулю q тогда и только тогда, когда q квадрат по модулю р . Если же оба числа p и q вида 4 n +3, то р квадрат по модулю q тогда и только тогда, когда q не является квадратом по модулю р .
Доказательство.
Поскольку
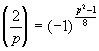, то формула из леммы 2 принимает вид:
.
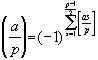Рассмотрим два множества:
S
={1,2,…, (
p
-1)/2} и
K
={1,2,…,(
q
-1)/2}.
Образуем ( p -1)/2 Ч ( q -1)/2 штук пар чисел ( qx,py ), где х пробегает S , a y пробегает К . Первая и вторая компонента одной пары никогда не совпадают, ибо из py = qx следует, что py кратно q . Но ведь это невозможно, так как ( p,q )=1 и, поскольку 0< y < q , то ( y , q )=1.
Положим, поэтому, ( p -1)/2 Ч ( q -1)/2= V 1 + V 2 , где V 1 – число пар, в которых первая компонента меньше второй ( qx < py ), V 2 – число пар, в которых вторая компонента меньше первой ( qx > py ).
Очевидно, что V 1 есть число пар, в которых x < ( p / q ) y . (Вообще-то, x Ј ( p -1)/2, но ( p / q ) y < p /2 т.к. y/q < 1/2 , следовательно [( p / q ) y ] Ј [ p/ 2]= ( p -1)/2, и неравенство x <( p / q ) y не противоречит неравенству x Ј ( p -1)/2.) Поэтому,
.
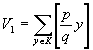Аналогично,
.
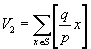Тогда равенство из леммы 2, отмеченное в начале этого доказательства, дает:
.
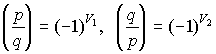Это означает, что
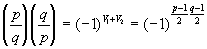, а это, собственно, и требовалось.
Ё
Барабанная дробь и фанфары!
Справедливости ради, следует отметить мелким шрифтом, что мы могли бы доказать закон взаимности в этом пункте сразу после леммы 1, но при этом упустили бы из виду важные свойства символа Лежандра, которые спрашивают на кандидатском экзамене по специальности “Алгебра, математическая логика и теория чисел”. Кроме того, “быстрое” доказательство закона взаимности страдает существенным недостатком – совершенно непонятно, как до него додуматься. А додумался до него немецкий математик Фердинанд Готхольд Эйзенштейн (1823–1852). Это доказательство, дословно почерпнутое из замечательной книжки Ж.П.Серра “Курс арифметики”, перед вами.
Тригонометрическая лемма. Пусть m – нечетное натуральное число. Тогда
.
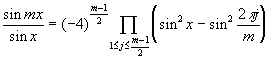Доказательство получается непосредственной проверкой. Например, по формуле Муавра, убеждаемся, что левая часть есть полином степени ( m -1)/2 от sin 2 x , корни которого есть sin 2 (2 p j/m ), где 1 Ј j Ј ( m -1)/2. Множитель (-4) ( m -1)/2 получается сравнением коэффициентов в левой и правой частях.
Доказательство закона взаимности.
Пусть
р
и
q
– два различных нечетных простых числа. По лемме Гаусса,
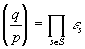. В силу равенства
qs
=
e
s
r
s
(обозначения леммы 1 сохранены), имеем:
.
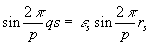(Синус-то функция нечетная, и знак можно вынести вперед.)
Перемножая эти равенства и учитывая, что отображение s ® r s биективно, получаем
.
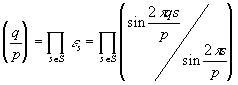Применим теперь тригонометрическую лемму при m = q :
.
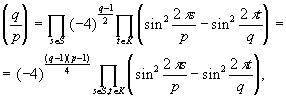где K ={1,2,…( q -1)/2}. Меняя роли q и р , точно так же получим:
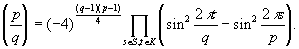
Множители в формулах для (
q/p
) и (
p/q
) одинаковы с точностью до знака. Число же противоположных знаков равно
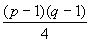, поэтому
.
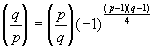Ё
На этом пункт 23 и с ним весь параграф, посвященный теории сравнений закончим. С удовлетворением отмечу, что если мы и не все познали в сравнении, то весьма немало. Примите мои сердечные поздравления.
Задачки
|
1.
Используя закон взаимности для “переворачивания” символа Лежандра, посчитайте:
2. Докажите, что число а одновременно является или квадратичным вычетом или квадратичным невычетом для всех простых чисел, входящих в арифметическую прогрессию 4 at + r , t =0,1,2…, где r - произвольное натуральное число, меньшее 4 а .) ** 3. Пусть p и q - простые числа и p + q =4 а . Докажите, что тогда число а является одновременно или квадратичным вычетом по модулям p и q или квадратичным невычетом. |