§5. Трансцендентные числа.
Пункт 26. Число e»2,718281828459045...
Матушка-природа подарила нам несколько замечательных констант, весьма неожиданно появляющихся при попытках математического выражения и записи законов разных наук. С одной из таких констант - “основанием натуральных логарифмов” - мы познакомимся поближе в этом пункте.
Когда-то давно я учился в средней школе № 110 г. Свердловска. В школе нам страшно повезло - судьба послала нам великого учителя, сухощавого математика на железной ноге Николая Ивановича Слободчакова, по прозвищу “Колываныч”. Самым загадочным образом хулиганы и двоечники становились у него отличниками, а математика - любимым предметом. Еще в восьмом классе Колываныч говорил нам: “Дети! Запомните, что основание натуральных логарифмов обозначается буквой e в честь Леонарда Ейлера, а запомнить его десятичные знаки очень просто. Два и семь - помнят все. Дальше - 1828, - год рождения Льва Николаевича Толстого. Дальше - снова 1828, - год рождения Жюль Верна, а если вы тупые, то - опять год рождения Толстого. Потом идут углы равнобедренного прямоугольного треугольника - 45, 90, 45. А что идет потом - я сам не знаю...”. Потом Николай Иванович доказал нам, что 2<e<3 и загробным голосом сказал: ” Число e - трансцендентно!”. Этим словом мы потом обзывались на переменках. Когда я поступил в университет, я узнал, что
;
;
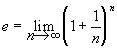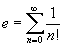e - основание показательной функции, являющейся
решением задачи Коши: yў
=y, y(0)=1;
и многое многое другое. Вразумительный ответ на вопрос, почему именно число e наиболее естественно взять за основание логарифмов, которые с таким основанием сразу становятся натуральными и пригодными к употреблению даже в период беременности, я нашел в книжке Ф. Клейна “Элементарная математика с точки зрения высшей”, том 1 , “Арифметика, алгебра, анализ”. Настоятельно советую ее прочитать, так как считаю, что с подобными книжками должен быть знаком каждый мало-мальски грамотный математик, ибо такие книжки составляют золотой фонд литературы о любимой нами науке.
Ряд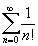 
сходится быстро (чего нельзя сказать про известные ряды, например, для числа
p). Это значит, что частичные суммы ряда 
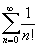, будучи рациональными числами, очень хорошо приближают число
e, поэтому естественно ожидать, что трансцендентность e
удастся доказать относительно легко (а исследование природы числа p
потребует гораздо больших усилий). Эти эвристические соображения действительно
находят свое подтверждение на практике, но не будем торопить события и начнем
по порядку.
Теорема 1. Число e иррационально.
Доказательство. Рассмотрим числа
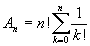и
.
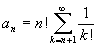Очевидно, что AnО N, an>0. Оценим an сверху:
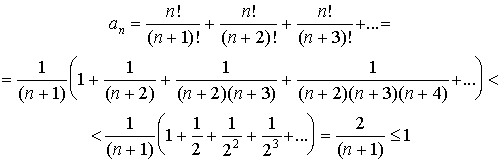
Итак, 0<an<1, т.е. an - всегда дробное число. Это означает, что при любом натуральном n, число n!e=An+an не является целым.
Пусть теперь e=p/q - рациональное число, p, qОN. Тогда q!e=q!p/q=(q-1!p) - целое число, что вопиюще противоречит факту, установленному тремя строчками выше.
Ё
Для доказательства трансцендентности героя этого пункта потребуются две леммы.
Лемма 1. Если g(x) – многочлен с целыми коэффициентами, то для любого kОN все коэффициенты его k-ой производной g(k)(x) делятся на k! .
Доказательство. Так как оператор d/dx линейный, то утверждение леммы достаточно проверить только для многочленов вида g(x)=xs, sі 0.
Если k>s, то g(k)(x)є 0 и k!|0.
Если kЈ
s, то
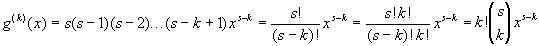
биномиальный коэффициент (sk) является целым числом и g(k)(x) опять-таки делится на k! нацело.
Ё
Ключевая идея доказательства трансцендентности числа e принадлежит Шарлю Эрмиту. Впрочем, идея Эрмита сработала и при доказательстве трансцендентности числа p, а также некоторых других чисел специального вида, но это уже заслуга других математиков. А трансцендентность непосредственно числа e доказал Эрмит в 1873 году и это был исторически первый решительный прорыв в познание природы замечательных констант. Слава Эрмиту!!!!! (Это четыре восклицательных знака и один факториал.)
Лемма 2 (Тождество Эрмита). Пусть f(x) - произвольный многочлен степени k с действительными коэффициентами,
F(x)=f(x)+ fў (x)+ fў ў (x)+…+ f(k)(x) - сумма всех его производных. Тогда для любого действительного (и даже комплексного, но нам это пока не понадобится) x выполнено:
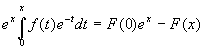
(Є)
Доказательство. Интегрируем по частям:
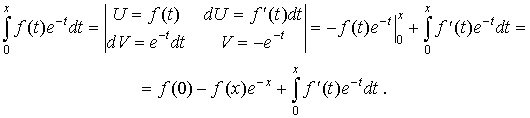
Интегр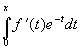ал
снова подвергнем процедуре
интегрирования по частям, потом этой прцедуре подвергнем интеграл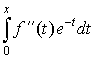 
и так далее. Терпеливо повторив эту процедуру всего k+1
раз, получим:
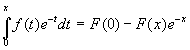
Ё
Теорема 2 (Эрмит, 1873). Число е трансцендентно.
Доказательство. От противного. Ну пусть е - алгебраическое, степени m. Тогда
amem+…+a1e+a0=0
для некоторого натурального m и некоторых целых am,…a1,a0, причем, очевидно, am№ 0 и a0№ 0. Подставим в тождество Эрмита (Є) вместо х целое число k, попросим k принимать по очереди значения 0, 1, ... , m; умножим каждое равенство
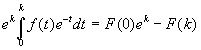
соответственно на ak, а затем все их сложим. Получим:
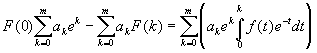
Так как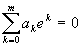 
(это наше противное предположение),
то выходит, что для любого многочлена f(x) должно быть выполнено
равенство:
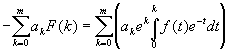
(ЄЄ)
Противоречие, которое углядел Эрмит в этом равенстве, сразу и не заметишь. Но Эрмит на то и Эрмит, чтобы превосходить интеллектом 15756 наугад вместе взятых китайцев и двух Мао Цзэ-дунов. Он сначала сердцем почуял, а потом и мозгами воткнулся, что за счет подходящего выбора многочлена f(x) можно сделать левую часть (ЄЄ) ненулевым целым числом, а правая часть при этом окажется между нулем и единицей.
Возьмем многочлен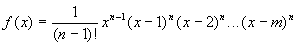 
, где n
определим позже (nО
N, и n будет очень большое).
Число 0 - корень кратности n-1 многочлена f(x), числа 1, 2, ..., m - корни кратности n, следовательно:
f(l)(0)=0, l=1,2,…,n-2
f(n-1)(0)=(-1)mn(m!)n
f(l)(k)=0, l=0,1, …,n-1; k=1,2,…,m
Рассмотрим j (x)=xn-1(x-1)n(x-2)n…(x-m)n - многочлен, ужасно похожий на f(x), но с целыми коэффициентами. По лемме 1, коэффициенты j (l)(x) - целые числа, делящиеся на l!, следовательно, при l і n, у производной j(l)(x) все коэффициенты - целые числа, делящиеся на n, т.к. j(l)(x) получается из j (l)(x) делением только на (n–1)! . Именно поэтому
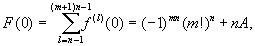
где А – подходящее целое число, а над знаком суммы стоит число (m+1)n-1 - степень многочлена f(x) и, хоть суммировать можно и до бесконечности, ненулевых производных у f(x) именно столько.
Аналогично
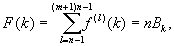
где Bk – подходящие целые числа, k = 1, 2, ..., m.
Пусть теперь nО N - любое целое число, удовлетворяющее условиям:
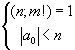
Снова рассмотрим равенство (ЄЄ):
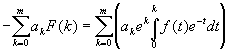
В сумме слева все слагаемые - суть целые числа, причем akF(k) при k = 1, 2, ..., m делится на n, а a0F(0) на n не делится. Это означает, что вся сумма, будучи целым числом, на nне делится, т.е. не является нулем. Следовательно,
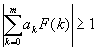
Уф-ф!
Оценим теперь правую часть равенства (ЄЄ). Ясно, чтоЅ x-kЅ Ј m на отрезке [0;m]. Поэтому на этом отрезке
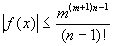
Тогда:
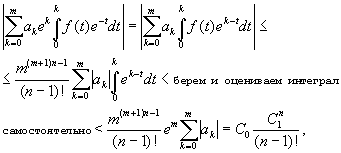
где константы C0 и C1 не зависят от n. Известно, что
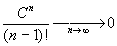
поэтому, при достаточно больших n, правая часть (ЄЄ) меньше единицы и равенство (ЄЄ) невозможно.
Ё
После прочтения такого серьезного доказательства я советую вам отдохнуть. Впереди предстоят еще более серьезные испытания.
| NS | СКАЗКА |
|
Жила была курочка Ряба и были у нее Дед да Баба. |
|