10 Теория функций комплексной переменной
10.1 Комплексные числа
В математике большую роль играют так
называемые обратные операции,
необходимость выполнения которых обычно приводит к расширению классов имеющихся
объектов.
Например, операция сложения. Когда-то
люди не знали отрицательных чисел. Складывая положительные числа, в ответе
всегда получались положительное число. Но обратная операция – вычитание –
привела к необходимости рассматривать числа отрицательные.
Операция умножения. Перемножая целые
числа, в ответе всегда получаем также целые числа. Обратная операция –
деление -приводит нас к необходимости рассматривать дробные, рациональные
числа.
Операция возведения в квадрат. Квадрат
рационального числа есть всегда также число рациональное. Но обратная операция –
извлечение квадратного корня – приводит к иррациональным числам (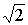 , например, не является рациональным числом). , например, не является рациональным числом).
Но та же самая операция извлечения
квадратного корня дает и еще один класс чисел. Как известно, квадрат любого
рационального числа есть число неотрицательное. Поэтому и квадратный корень
можно извлечь только из неотрицательных чисел (например, 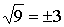 ). А как быть с ). А как быть с 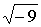 ? Чему он равен? Ведь нет такого рационального числа,
квадрат которого был бы равен – 9. ? Чему он равен? Ведь нет такого рационального числа,
квадрат которого был бы равен – 9.
Но,
как говорится, если нельзя, но очень хочется, то можно. И желание извлекать
корни из отрицательных чисел привело к новому классу чисел, называемых комплексными числами. Для их
рассмотрения оказалось достаточным ввести всего лишь одно новое число
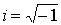 , ,
которое
называется мнимой единицей. Считается, что это «число»
обладает всеми свойствами обычных чисел и имеет всего одно единственное новое
свойство
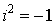 , ,
так что,
например, 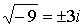 . Числа, содержащие i,
называются комплексными числами. Без них немыслима современная математика. . Числа, содержащие i,
называются комплексными числами. Без них немыслима современная математика.
10.1.1 Алгебраическая форма комплексных чисел
Пусть x и y – обычные числа. Число вида
z=x+iy
называется
комплексным числом в алгебраической
форме.
x называют вещественной или действительной частью числа z и
обозначают так: 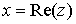 ; y называют
мнимой частью числа z и обозначают так: ; y называют
мнимой частью числа z и обозначают так: 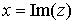 . Число . Число 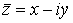 называют комплексно сопряженным числу z. Действует следующее общее правило: «чтобы получить число,
комплексно сопряженное данному, надо в нем заменить i на –i ». называют комплексно сопряженным числу z. Действует следующее общее правило: «чтобы получить число,
комплексно сопряженное данному, надо в нем заменить i на –i ».
Рассмотрим операции над комплексными
числами в алгебраической форме. Пусть даны два комплексных числа 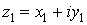 и и 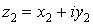 . .
Равенство
и сравнение комплексных чисел.
Два комплексных числа считаются
равными, если у них равны вещественные и мнимые части:
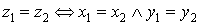 . .
Но вот операции типа «больше» и
«меньше» для комплексных чисел не имеют
смысла, то есть бессмысленно писать 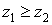 или или 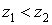 . Совершенно непонятно, что больше . Совершенно непонятно, что больше 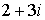 или или 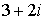 . Комплексные
числа не упорядочены. . Комплексные
числа не упорядочены.
Сложение
и вычитание.
Сложение и вычитание двух комплексных
чисел определяются совершенно естественно
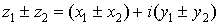 , ,
то есть надо
сложить (или вычесть) отдельно вещественные и мнимые части чисел.
Умножение.
Умножение двух комплексных чисел производится как умножение обычных
чисел, надо лишь помнить, что 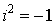 : :
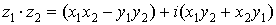 . .
Деление.
Для деления комплексных чисел полезно
запомнить следующее правило: чтобы разделить два комплексных числа друг на
друга надо числитель и знаменатель умножить на число, комплексно сопряженное
знаменателю. Тогда легко получить, что
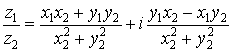 . .
10.1.2 Геометрическая
интерпретация комплексных чисел.

Рис. 10.1 Геометрическая
интерпретация комплексного числа
Пусть имеется комплексное число 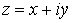 . Возьмем на плоскости декартову систему координат и
комплексному числу z поставим в соответствие точку на
этой плоскости с координатами (x, y) (см.
рис. 10.1). Таким образом, геометрически комплексные числа – это точки на
плоскости (вспомните, что вещественные числа – это точки на числовой оси). Саму
плоскость называют плоскостью комплексной переменной z. . Возьмем на плоскости декартову систему координат и
комплексному числу z поставим в соответствие точку на
этой плоскости с координатами (x, y) (см.
рис. 10.1). Таким образом, геометрически комплексные числа – это точки на
плоскости (вспомните, что вещественные числа – это точки на числовой оси). Саму
плоскость называют плоскостью комплексной переменной z.
10.1.3 Тригонометрическая форма комплексного
числа.
С геометрической интерпретацией связана
и еще одна форма записи комплексных чисел, называемая тригонометрической формой
их записи.
Соединим точку (x, y) с началом координат отрезком прямой. Длина этого отрезка r называется модулем комплексного числа z и
обозначается | z | или mod(z).
Угол
j,
который этот отрезок образует с осью ОХ,
называется аргументом комплексного
числа z и обозначается arg(z).
Из
рисунка ясно, что имеют место соотношения
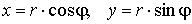 , ,
или наоборот
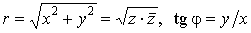 . .
Теперь мы можем
записать 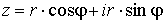 или окончательно или окончательно
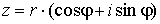 . .
Эта форма и
получила название комплексного числа в тригонометрической форме.
Операции
над комплексными числами в тригонометрической форме.
Пусть
имеются два комплексных числа 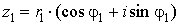 и и 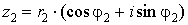 . .
Умножение.
Легко вывести, что
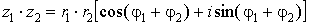 , ,
то есть при
перемножении комплексных чисел их модули перемножаются, а аргументы –
складываются.
Деление.
Можно вывести, что
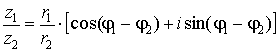 , ,
то есть при
делении комплексных чисел их модули делятся, а аргументы – вычитаются.
Возведение
в степень.
Пусть
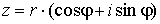 . Тогда имеет место формула . Тогда имеет место формула
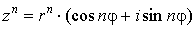 , ,
то есть при
возведении в степень модуль возводится в эту степень, а аргумент – умножается на нее.
Извлечение
корня.
Пусть снова 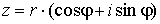 . Тогда имеет место формула . Тогда имеет место формула
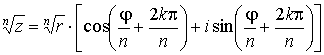 , ,
с 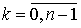 . Таким образом, корень
n-й степени из
комплексного числа имеет ровно n различных значений. . Таким образом, корень
n-й степени из
комплексного числа имеет ровно n различных значений.
10.1.4 Формула
Эйлера. Показательная форма комплексного числа.
Одна из важнейших формул
математического анализа – формула Эйлера – имеет вид
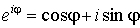 . .
С учетом
тригонометрической формы комплексного числа его теперь можно представить в виде
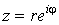 , ,
или, с учетом
того, что аргумент определяется с точностью до 2p,
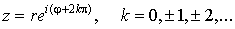 . .
Эта форма записи помогает, например, определить логарифм комплексного
числа
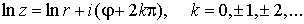 . .
10.2 Функция
комплексной переменной
Представим
себе, что есть две плоскости комплексной переменной, одна – плоскость
комплексной переменной 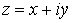 , другая – плоскость комплексной переменной , другая – плоскость комплексной переменной 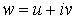 (см. рис. 10.2). (см. рис. 10.2).
Правило, которое каждой точке z из некоторой области G ставит
в соответствие точку w, называется функцией комплексной
переменной и обозначается 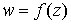 . .
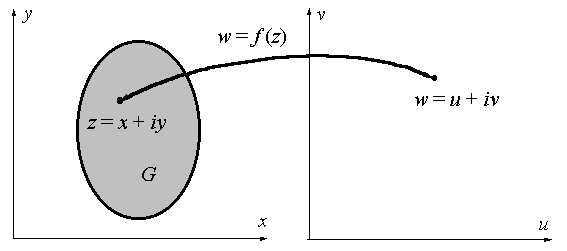
Рис. 10.2 К определению функции
комплексной переменной
Подчеркнем, что и аргумент z и значение функции w – комплексные переменные. Так как 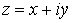 и и 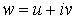 , то задание , то задание 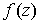 сводится
фактически к заданию двух функций сводится
фактически к заданию двух функций 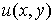 и и 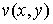 от двух переменных x и y, то есть от двух переменных x и y, то есть 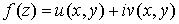 . .
Основные понятия теории функций –
предел функции, непрерывность функции и соответствующие им теоремы переносятся
на функции комплексной переменной. Отличия начинаются в понятии производной.
10.3 Производная
от функции комплексной переменной
Пусть задана функция 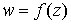 . Говорят что у . Говорят что у 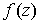 существует
производная в точке z, если существует существует
производная в точке z, если существует
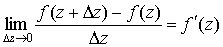 . .
Определение.
Если 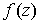 имеет
производную в каждой точке области G, то она называется аналитической в области G. имеет
производную в каждой точке области G, то она называется аналитической в области G.
Выясним геометрический смысл
производной. Рассмотрим на плоскости z бесконечно малый
отрезок, соединяющий точки z и Dz. Тогда длина этого отрезка есть |Dz|, а arg Dz есть угол, который этот отрезок образует с
осью OX (см. рис. 10.3).
Аналогично, на плоскости w бесконечно малый отрезок, соединяющий точки w и Dw. Тогда длина этого отрезка есть |Dw|, а arg Dw есть угол, который
этот отрезок образует с осью OU.
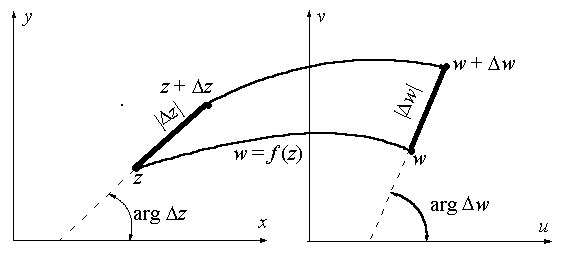
Рис. 10.3 Геометрический смысл
производной от функции комплексной переменной
А теперь вспомним, что 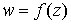 , , 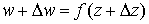 , так что , так что 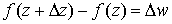 . Тогда получим . Тогда получим
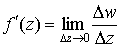 . .
Отсюда
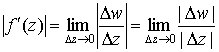 . .
Отношение 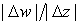 есть отношение
длин отрезков есть отношение
длин отрезков 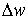 и и 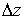 . Таким образом, . Таким образом, 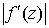 есть коэффициент растяжения бесконечно
малого отрезка при его отображении с плоскости z на
плоскость w. есть коэффициент растяжения бесконечно
малого отрезка при его отображении с плоскости z на
плоскость w.
Далее, так как
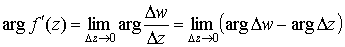 , ,
то 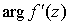 есть угол поворота бесконечно малого отрезка
при его отображении с плоскости z на плоскость w. Заметим, что этот угол поворота не зависит от есть угол поворота бесконечно малого отрезка
при его отображении с плоскости z на плоскость w. Заметим, что этот угол поворота не зависит от 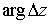 , то есть от направления отрезка , то есть от направления отрезка 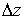 . .
10.4 Условия Коши-Римана
Условия
Коши-Римана дают необходимые и достаточные условия существования производной у функции
комплексной переменной.
Пусть дана функция комплексной
переменной 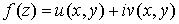 , у которой в
точке , у которой в
точке 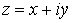 существует
производная существует
производная 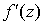 . Тогда в этой
точке выполнены соотношения . Тогда в этой
точке выполнены соотношения
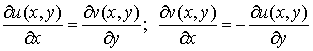 , ,
которые и
называются условиями Коши-Римана. Если функции 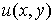 и и 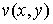 дифференцируемы в точке дифференцируемы в точке 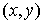 то эти условия достаточны
для существования то эти условия достаточны
для существования 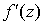 . .
10.5 Интеграл
от функции комплексной переменной
Пусть
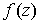 – функция
комплексной переменной z и C – некоторая
кривая на плоскости z (см. рис.
10.4). – функция
комплексной переменной z и C – некоторая
кривая на плоскости z (см. рис.
10.4).

Рис. 10.4 К построению интеграла от
функции комплексной переменной
Разобьем всю кривую на кусочки точками 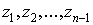 так, что начало
кривой есть точка так, что начало
кривой есть точка 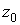 , а конец – точка , а конец – точка 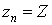 . На каждом кусочке произвольным образом выберем
среднюю точку . На каждом кусочке произвольным образом выберем
среднюю точку 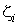 и составим
интегральную сумму и составим
интегральную сумму
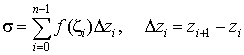 . .
Пусть 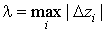 . Если существует . Если существует 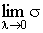 и этот предел
не зависит от способа разбиения кривой С
на кусочки и от способа выбора средней точки, то он называется интегралом от
функции и этот предел
не зависит от способа разбиения кривой С
на кусочки и от способа выбора средней точки, то он называется интегралом от
функции 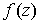 по кривой С: по кривой С:
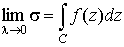 . .
Важнейшее неравенство на этот интеграл
имеет вид
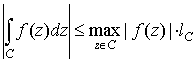 , ,
где 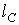 есть длина
кривой С. есть длина
кривой С.
Теорема.
Если 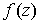 аналитична в
односвязной области G, то аналитична в
односвязной области G, то 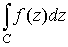 по всем кривым С, лежащим в G, зависит
только от начала и конца кривой и не зависит от вида этой кривой. по всем кривым С, лежащим в G, зависит
только от начала и конца кривой и не зависит от вида этой кривой.
10.6 Интегральные
формулы Коши
Приведем
две основные формулы, касающиеся аналитических функций.
Теорема
1. Пусть 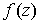 аналитична в
односвязной области G. Тогда для любой точки аналитична в
односвязной области G. Тогда для любой точки 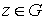 имеет место
формула имеет место
формула
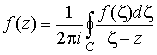 , ,
где C – любой простой контур, лежащий в G и
охватывающий z. В частности, в качестве контура С может быть взята граница области G.
Эта теорема устанавливает очень
интересное свойство аналитической функции: ее значения на границе области
полностью определяют ее значения внутри области.
Теорема
2. Если 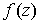 аналитична в
односвязной области G, то в этой области у нее
существуют производные всех порядков,
причем аналитична в
односвязной области G, то в этой области у нее
существуют производные всех порядков,
причем
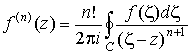 , ,
где C – любой простой контур, лежащий в G и
охватывающий z. В частности, в качестве контура С может быть взята граница области G.
Эта теорема устанавливает еще одно
очень интересное свойство функций комплексной переменной, не имеющее аналога
для функций вещественной переменной: существование первой производной
гарантирует существование всех остальных производных.
Неравенство
Коши. Обозначим через 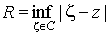 минимальное расстояние
от точки z до контура С, и пусть минимальное расстояние
от точки z до контура С, и пусть 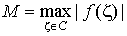 . Тогда имеет место неравенство . Тогда имеет место неравенство
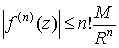 , ,
которое также
носит имя Коши.
|