12. Теория вычетов
12.1 Особые точки аналитических функций
Определение. Точка а называется особой точкой функции
 , если в этой точке функция имеет разрыв или у нее не
существует производная. , если в этой точке функция имеет разрыв или у нее не
существует производная.
Точка а называется изолированной особой точкой функции  , если существует такое , если существует такое 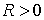 , что в кольце , что в кольце 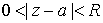 функция
аналитична. функция
аналитична.
В
дальнейшем рассматриваются только изолированные особые точки.
Пусть
а – изолированная особая точка
функции  . .
Определение 1. Точка а называется устранимой особой точкой функции  , если существует конечный предел , если существует конечный предел 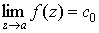 . .
Теорема
1. Для того, чтобы а была
устранимой особой точкой функции  необходимо и
достаточно, чтобы в разложении необходимо и
достаточно, чтобы в разложении  в кольце в кольце 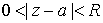 в ряд Лорана в
нем отсутствовала главная часть. в ряд Лорана в
нем отсутствовала главная часть.
Если положить 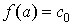 , то особенность исчезает. , то особенность исчезает.
Определение
2. Точка а называется полюсом функции  , если , если 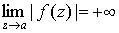 . .
Теорема
2. Для того, чтобы а была полюсом
функции  необходимо и
достаточно, чтобы в разложении необходимо и
достаточно, чтобы в разложении  в кольце в кольце 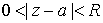 в ряд Лорана в
главной части было конечное число слагаемых. в ряд Лорана в
главной части было конечное число слагаемых.
Замечание.
Если главная часть начинается с члена, содержащего 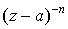 , то говорят, что точка а есть полюс n-го порядка. Если n=1, то полюс называется простым. , то говорят, что точка а есть полюс n-го порядка. Если n=1, то полюс называется простым.
Определение
3. Если 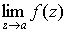 не существует,
то точка а называется существенно особой точкой функции не существует,
то точка а называется существенно особой точкой функции  . .
Теорема
3. Для того, чтобы а была существенно
особой точкой функции  необходимо и
достаточно, чтобы в разложении необходимо и
достаточно, чтобы в разложении  в кольце в кольце 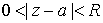 в ряд Лорана в
главной части было бесконечное число слагаемых. в ряд Лорана в
главной части было бесконечное число слагаемых.
12.2 Вычеты
в особых точках
Пусть
а – изолированная особая точка
функции  . .
Теорема.
Интегралы по всем простым контурам, окружающим особую точку, равны между
собой.
Таким образом, интегралы по простым
контурам, окружающим особую точку, являются характеристикой точки, а не контура.
Определение. Пусть G -
любой простой контур, окружающий особую точку а. Величина
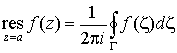
называется вычетом функции  в точке а и обозначается символом в точке а и обозначается символом 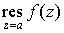 . .
Сравним это выражение с выражением для
коэффициентов ряда Лорана функции  : :
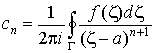 . .
Если взять n = – 1, то получим
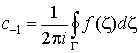 , ,
и получается, что 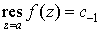 . .
Итак:
Вычетом функции  в точке а называется величина в точке а называется величина 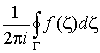 , где интеграл берется по любому простому контуру,
окружающему особую точку. Численно вычет
равен коэффициенту , где интеграл берется по любому простому контуру,
окружающему особую точку. Численно вычет
равен коэффициенту 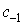 в разложении
функции в разложении
функции  в ряд Лорана в
окрестности точки а. в ряд Лорана в
окрестности точки а.
12.3 Вычисление
вычетов
1. Пусть
а есть простой полюс функции  . Тогда . Тогда
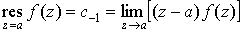 . .
Частный
случай. Пусть  имеет вид имеет вид 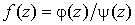 , причем , причем 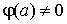 , , 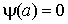 , но , но 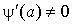 . Тогда . Тогда
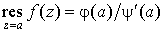 . .
Этой формулой на
практике приходится пользоваться чаще всего.
2. Пусть а есть полюс n-го порядка функции  . Тогда . Тогда
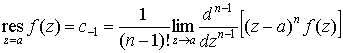 . .
Отметим самый принципиальный момент:
хотя вычет и определяется через интеграл, но вычисляются они без всяких
интегралов. Поэтому не вычеты вычисляются
через интегралы, а наоборот – интегралы
вычисляются через вычеты! И это – самое главное, так как именно через
вычеты вычисляется огромное количество несобственных интегралов, которые
относятся к классу неберущихся интегралов, то есть у которых первообразная не
принадлежит к классу элементарных функций.
12.4 Основная
теорема теории вычетов
Теорема.
Пусть  - аналитическая
внутри контура С функция за исключением
конечного числа изолированных особых точек - аналитическая
внутри контура С функция за исключением
конечного числа изолированных особых точек 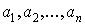 . Тогда . Тогда
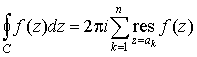 . .
Именно эта теорема дает возможность вычислять целые классы несобственных
интегралов через вычеты функции  . Приведем только простейшую из соответствующих
теорем. . Приведем только простейшую из соответствующих
теорем.
12.5 Вычисление
интегралов вида 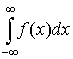
Теорема.
Пусть  есть функция,
аналитическая в верхней полуплоскости есть функция,
аналитическая в верхней полуплоскости 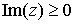 за исключением
конечного числа изолированных особых точек, и существуют такие за исключением
конечного числа изолированных особых точек, и существуют такие 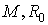 и и 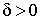 , что , что
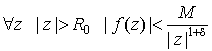 , ,
где сумма
берется по всем особым точкам, лежащим в верхней полуплоскости 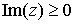 . .
Тогда
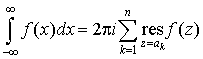 . .
|