3. Производная
3.1 Определение
производной
Пусть функция f(x) непрерывна в
точке x. Тогда производной 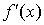 от этой функции
в точке x, называется предел (разумеется,
если он существует) от этой функции
в точке x, называется предел (разумеется,
если он существует)
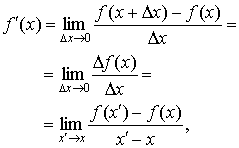
где 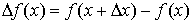 - приращение
функции. - приращение
функции.
Геометрический смысл производной
состоит в том, что численно она равна тангенсу угла между касательной,
проведенной к кривой в точке x, и осью абсцисс OX (см.
рис. 3.1).
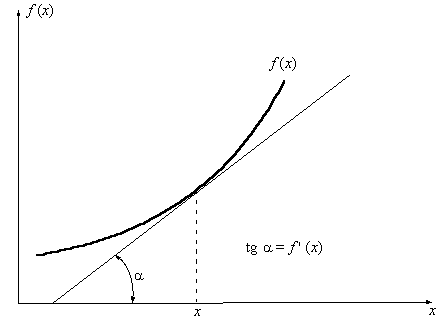
Рис. 3.1 Геометрический смысл
производной.
3.2 Правила
вычисления производных (алгебра производных)
Ниже приводятся основные формулы,
служащие для вычисления производных.
1. 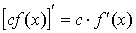 ; ;
2. 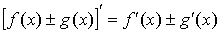 ; ;
3. 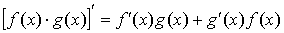 ; ;
4. 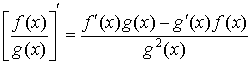 ; ;
5.
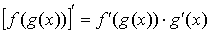 ; ;
6. 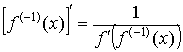 . .
3.3 Таблица производных
Ниже приводится таблица производных от
элементарных функций, которую надо знать так же хорошо, как таблицу умножения.
|
Функция
|
Производная
|
Функция
|
Производная
|
|
с
|
0
|
ctg x
|
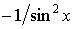
|
|
xm
|
mxm-1
|
arc sin x
|
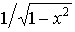
|
|
ax
|
ax×ln a
|
arc cos x
|
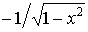
|
|
ex
|
ex
|
arc tg x
|
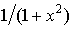
|
|
loga
x
|
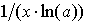
|
arc ctg x
|
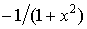
|
|
ln x
|
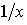
|
sh x
|
ch x
|
|
sin x
|
cos x
|
ch x
|
sh x
|
|
cos x
|
- sin x
|
th x
|
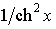
|
|
tg x
|
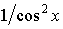
|
cth x
|
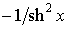
|
3.4 Односторонние производные
Выражение
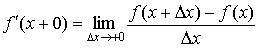
называется
производной справа функции f(x) в точке x. Аналогично, выражение
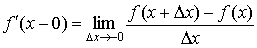
называется
производной слева в этой же точке.
Если 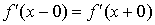 , то в точке x существует , то в точке x существует 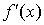 ; если же ; если же 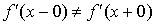 , то в точке x производной , то в точке x производной 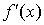 не существует и
график функции имеет излом; в этой точке имеется две касательных (см. рис. 3.2). не существует и
график функции имеет излом; в этой точке имеется две касательных (см. рис. 3.2).
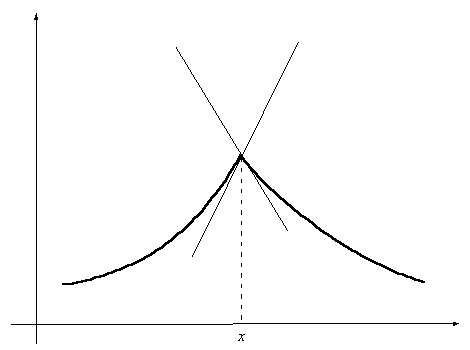
Рис. 3.2 Вид графика функции в
окрестности точки,
в которой односторонние производные
не равны друг другу.
3.5 Теоремы
о функциях, имеющих производную
Теорема
Ферма. Пусть f(x) определена
в [a, b] и во внутренней точке x0 этого
промежутка принимает наибольшее (наименьшее) значение. Если в этой точке существует 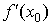 , то , то 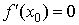 . .
Геометрический смысл этой теоремы
состоит в том, что в точке экстремума касательная к кривой параллельна оси
абсцисс (см. рис. 3.3).
Формулы
Коши и Лагранжа
Теорема.
Пусть
1.
f(x) и g(x) определены и непрерывны на [a, b];
2.
существуют 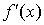 и и 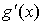 по крайней мере
в (a, b); по крайней мере
в (a, b);
3.
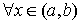 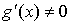 . .
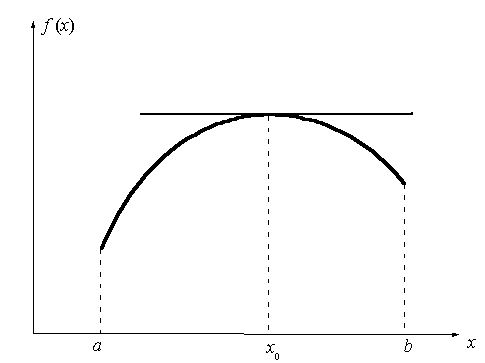
Рис. 3.3 Геометрический смысл теоремы Ферма
Тогда существует
точка 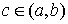 такая, что такая, что
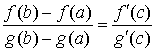 . .
Эта формула называется формулой Коши. Заметьте, что точек с может быть несколько.
Если взять 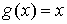 , то формула Коши приобретает вид , то формула Коши приобретает вид
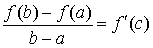 , ,
которая
называется формулой Лагранжа. Ее
геометрическая интерпретация приведена на рис. 3.4.
Обычно формулу Лагранжа пишут в виде
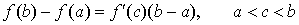 . .
Она является
одной из самых популярных формул математического анализа.
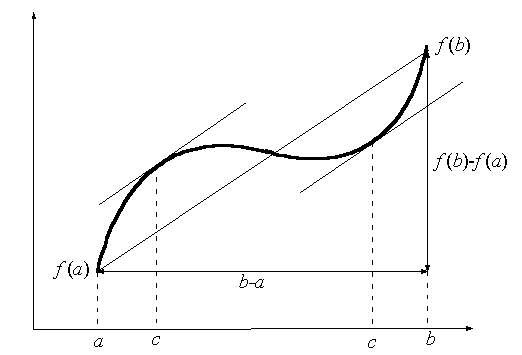
Рис. 3.4 Геометрическая интерпретация
формулы Лагранжа
3.6 Производные высших
порядков
Производная от производной первого порядка называется производной второго
порядка. Производная от производной второго порядка называется производной
третьего порядка. Вообще, производной n-го порядка называется
производная от производной n -1-го
порядка. По определению сама функция считается производной нулевого порядка от
самой себя.
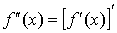 ; ; 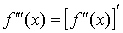 ; ...
, ; ...
, 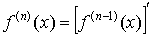 . . 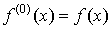 . .
Относительно
этих производных надо знать формулу
Лейбница
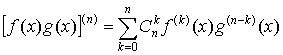 . .
3.7
Дифференциал
Определение.
Функция f(x)
называется дифференцируемой в точке х, если ее приращение 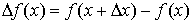 может быть
представлено в виде может быть
представлено в виде
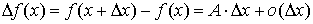 . .
Линейная часть
приращения функции, то есть слагаемое 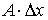 называется дифференциалом функции в точке х и обозначается так: называется дифференциалом функции в точке х и обозначается так: 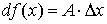 . .
Теорема.
Для того, чтобы функция f(x) была дифференцируемой
в точке х, необходимо и достаточно, чтобы она имела производную в этой
точке. При этом 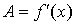 , , 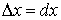 и и 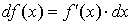 . .
Геометрический смысл дифференциала
изображен на рис. 3.5. Заметьте, что производная есть отношение дифференциала функции к дифференциалу независимой
переменной:
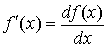 . .
Это – самая обычная дробь.
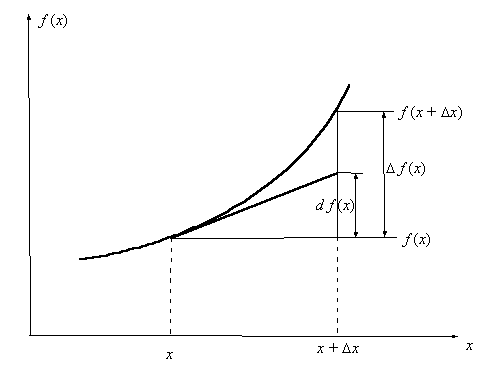
Рис. 3.5 Геометрический смысл
дифференциала.
Свойства
операции дифференцирования.
1. 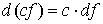 ; ;
2. 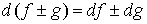 ; ;
3. 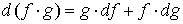 ; ;
4. 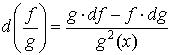 ; ;
5. 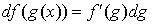 . .
Дифференциалы высших порядков.
Дифференциал
от дифференциала первого порядка называется дифференциалом второго порядка.
Дифференциал от дифференциала второго порядка называется дифференциалом
третьего порядка. Вообще, дифференциалом
n-го порядка
называется дифференциал от дифференциала n -1-го
порядка. Имеют место следующие формулы:
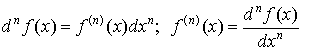 . .
3.8 Формула
Тейлора
Пусть функция f(x) имеет в точке x0 все
производные до n-го порядка включительно. Тогда ее
можно представить в виде
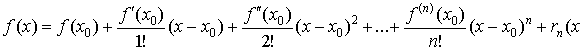 ). ).
Эта формула
носит название формулы Тейлора и она
является одной из важнейших формул математического анализа. Слагаемое 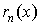 называется остаточным членом. Записанная в виде называется остаточным членом. Записанная в виде
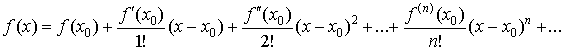
она называется рядом Тейлора.
Остаточный
член в форме Пеано имеет вид 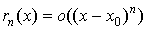 . Практического значения эта формула не имеет, но
очень полезна пр теоретическом исследовании. . Практического значения эта формула не имеет, но
очень полезна пр теоретическом исследовании.
Остаточный
член в форме Лагранжа имеет вид
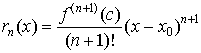 , ,
где x0 < c< x. Она используется для
количественной оценки погрешности представления функции f(x) формулой Тейлора.
3.9 Разложение
в ряд Тейлора некоторых функций
Ниже приводятся самые популярные
разложения в ряд Тейлора.
1. 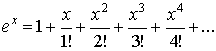 ; ;
2. 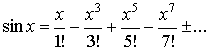 ; ;
3. 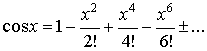 ; ;
4. 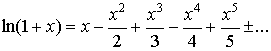
5. 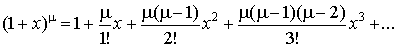 . .
При целой степени последняя формула превращается в так называемый бином Ньютона
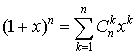 , ,
где 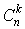 - биномиальный коэффициент - биномиальный коэффициент 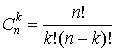 . .
3.10 Правило
Лопиталя
Правило Лопиталя используется для
раскрытия неопределенностей типа 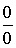 и и 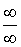 . .
Теорема
1. Пусть f(x) и g(x)
1.
определены в (a, b);
2.
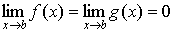 ; ;
3.
в (a, b)
существуют 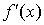 и и 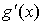 , причем , причем 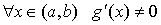 ; ;
4.
существует 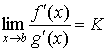 . .
Тогда существует
и 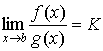 . .
Теорема
2. Пусть f(x) и g(x)
1.
определены в (a, b);
2.
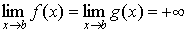 ; ;
3.
в (a, b)
существуют 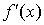 и и 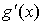 , причем , причем 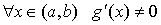 ; ;
4.
существует 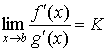 . .
Тогда существует
и 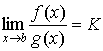 . .
Заметьте, что b может
быть равно +¥.
Короче говоря, правило Лопиталя
утверждает, что предел отношения функций равен пределу отношения их
производных.
3.11 Связь
производной и монотонности функции
Теорема.
Пусть f(x) определена
и непрерывна на промежутке 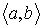 и внутри него
имеет конечную производную. Для того, чтобы f(x)
монотонно возрастала (убывала), необходимо и достаточно, чтобы было и внутри него
имеет конечную производную. Для того, чтобы f(x)
монотонно возрастала (убывала), необходимо и достаточно, чтобы было 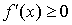 ( (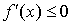 ). ).
3.12 Экстремумы
функции
Определение.
Говорят, что функция f(x) имеет в
точке x0 локальный
максимум (минимум) если
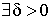 такое, что такое, что 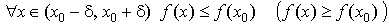 . .
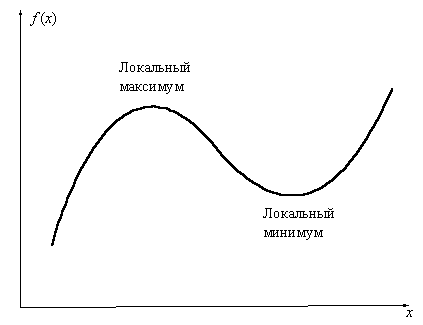
Рис. 3.6 Вид локальных максимума и
минимума
Приблизительный вид локального максимума и локального минимума приведен
на рис. 3.6. Оба эти термина объединяют термином локальный экстремум.
Необходимое условие экстремума дается
теоремой Ферма. Если во внутренней точке x0 функция f(x) имеет локальный экстремум, то в
ней 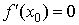 . .
Достаточное условие экстремума. Пусть
в точке x0 выполнено условие 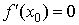 . Найдем первую по порядку старшинства производную,
отличную от нуля: . Найдем первую по порядку старшинства производную,
отличную от нуля: 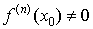 . Тогда возможны следующие варианты. . Тогда возможны следующие варианты.
а) n=2m – четное
число. Тогда в точке x0 имеет место локальный
экстремум, причем если 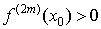 , то в точке x0 – локальный
максимум, а если , то в точке x0 – локальный
максимум, а если 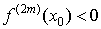 , то в точке x0 – локальный
минимум. , то в точке x0 – локальный
минимум.
б) n=2m+1 – нечетное
число. Тогда в точке x0 локального экстремума
нет (это – точка перегиба).
3.13 Выпуклые и вогнутые
функции
Определение 1. Функция f(x) называется выпуклой на отрезке [a, b], если 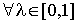 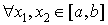 выполнено
условие выполнено
условие
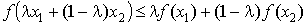 . .
Примерный вид графика выпуклой функции
приведен на рис. 3.7. Его отличительной особенностью является то, что график
выпуклой функции лежит под хордой,
соединяющей две любые ее точки.
Определение 2. Функция f(x) называется вогнутой на отрезке [a, b], если 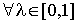 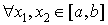 выполнено
условие выполнено
условие
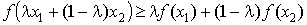 . .
Примерный вид графика вогнутой функции
приведен на рис. 3.8. Его отличительной особенностью является то, что график
вогнутой функции лежит над хордой,
соединяющей две любые ее точки.

Рис. 3.7 Вид графика выпуклой функции

Рис. 3.8 Вид графика вогнутой функции
Отметим
еще одно свойство этих графиков: график выпуклой
функции лежит над касательной,
проведенной к любой ее точке, а график вогнутой
функции – под касательной.
Неравенство
Иенсена.
Пусть f(x) – выпуклая функция
и пусть 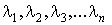 удовлетворяют условиям: удовлетворяют условиям:
a) 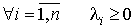 ; ;
b)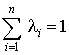 . .
Тогда
имеет место неравенство
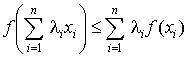 . .
Для вогнутой функции неравенство повернуто
в противоположную сторону.
Связь
выпуклости (вогнутости) функции с поведением ее производной
Теорема.
Пусть f(x)
определена и непрерывна на [a, b] и 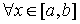 имеет конечную
производную. Для того, чтобы f(x) была
выпуклой (вогнутой) необходимо и достаточно, чтобы имеет конечную
производную. Для того, чтобы f(x) была
выпуклой (вогнутой) необходимо и достаточно, чтобы 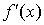 монотонно
возрастала (убывала). монотонно
возрастала (убывала).
Следствие.
Пусть f(x) и 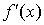 непрерывны на [a, b] и непрерывны на [a, b] и 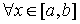 существует существует 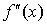 . Тогда для того, чтобы f(x) была выпуклой (вогнутой) необходимо и достаточно, чтобы . Тогда для того, чтобы f(x) была выпуклой (вогнутой) необходимо и достаточно, чтобы
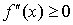 ( (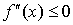 ). ).
3.14 Точка
перегиба
Определение.
Точка x0 называется точкой перегиба функции f(x) если она отделяет участок, где f(x) выпукла от участка, где f(x) вогнута.

Рис. 3.9 Вид графика функции в
окрестности точки перегиба
Вид графика функции в окрестности точки
перегиба приведен на рис. 3.9. Обратите внимание на то, что касательная
проведенная к кривой в точке перегиба пересекает
кривую.
Необходимое
условие точки перегиба. Если x0 – точка
перегиба функции f(x), то в
ней выполняется условие 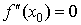 . .
Достаточное условие точки перегиба. Если
выполнено условие 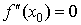 , то это еще не означает, что x0 – точка
перегиба функции f(x). Для
выяснения того, как выглядит график функции в окрестности этой точки надо найти
первую по порядку старшинства производную, отличную от нуля , то это еще не означает, что x0 – точка
перегиба функции f(x). Для
выяснения того, как выглядит график функции в окрестности этой точки надо найти
первую по порядку старшинства производную, отличную от нуля 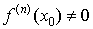 , причем должно быть , причем должно быть 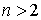 . Если это будет производная нечетного порядка, n=2m+1, то x0 есть точка перегиба функции f(x). Если же это будет производная четного порядка n=2m, то x0 есть точка локального
экстремума функции f(x). . Если это будет производная нечетного порядка, n=2m+1, то x0 есть точка перегиба функции f(x). Если же это будет производная четного порядка n=2m, то x0 есть точка локального
экстремума функции f(x).
|