6. Несобственные
интегралы
6.1 Определение и
свойства несобственных интегралов первого рода
Пусть
.
Функция 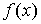 определена на определена на 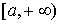 ; ;
2.
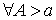 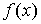 интегрируема на интегрируема на
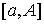 . .
Предел вида
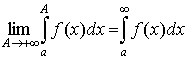
называется несобственным интегралом первого рода.
Если этот предел существует и конечен, то говорят, что  сходится или существует. Если это предел не существует
или бесконечен, то говорят, что сходится или существует. Если это предел не существует
или бесконечен, то говорят, что  расходится или не существует. расходится или не существует.
Аналогично,
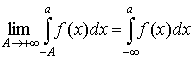 , ,
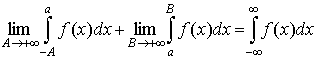 . .
Предел вида 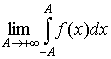 называется главным значением несобственного
интеграла называется главным значением несобственного
интеграла 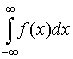 и обозначается
так и обозначается
так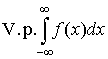 . .
Свойства.
1. Если существует  , то , то  существует существует 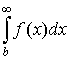 . При этом . При этом
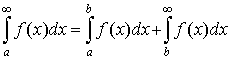 . .
2. Если существует  , то , то 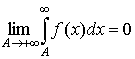 . .
3. Если существует  , то существует , то существует 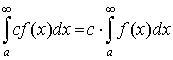 . .
4. Если существуют  и и 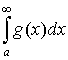 , то существует , то существует
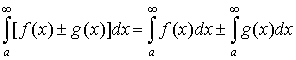 . .
6.2 Несобственные
интегралы первого рода от неотрицательных функций
В этом разделе всюду предполагается,
что  и и 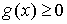 . .
Теорема
1. Если 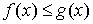 , то , то
1. если 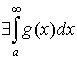 , то , то 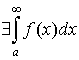 ; ;
2. если 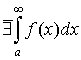 , то , то 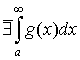 . .
Теорема
2. Если существует
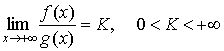 , ,
то интегралы  и и 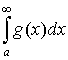 сходятся или расходятся
одновременно. сходятся или расходятся
одновременно.
Практический
признак сходимости.
Пусть
при 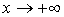 существует существует 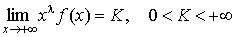 . Тогда . Тогда
если 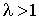 , то , то  сходится; сходится;
если 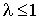 , то , то  расходится. расходится.
6.3 Несобственные
интегралы первого рода от функций произвольного знака
В
данном разделе функции 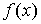 и и 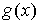 могут иметь
произвольный знак. могут иметь
произвольный знак.
Теорема.
Если существует 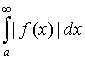 , то существует и , то существует и  . .
Определение.
Если существует 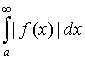 , то интеграл , то интеграл  называется абсолютно сходящимся. называется абсолютно сходящимся.
Если существует  , но , но 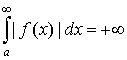 , то интеграл , то интеграл  называется неабсолютно сходящимся. называется неабсолютно сходящимся.
Признак
Дирихле. Пусть
1. 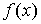 интегрируема в
любом интегрируема в
любом 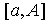 , причем , причем 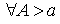
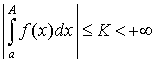 ; ;
2. При 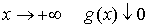 . .
Тогда 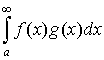 сходится. сходится.
Следствие.
Если при 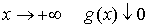 , то существуют , то существуют 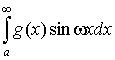 и и 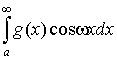 (последний – при (последний – при
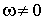 ). ).
6.4 Несобственные
интегралы второго рода
Определение.
Точка с называется особой точкой функции f(x), если 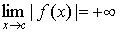 или этот предел
не существует. Ниже рассматривается лишь первый случай. или этот предел
не существует. Ниже рассматривается лишь первый случай.
Пусть b есть
особая точка функции f(x) и для
любого 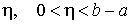 эта функция
интегрируема на отрезке эта функция
интегрируема на отрезке 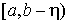 . Тогда предел . Тогда предел
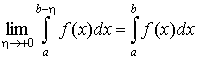
называется несобственным интегралом второго рода. Если
этот предел существует и конечен, то говорят, что интеграл сходится или
существует, если же этот предел равен бесконечности, то интеграл расходится,
или не существует.
Аналогично, если особой точкой является
а, то несобственный интеграл второго
рода определяется так
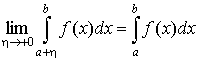 . .
Наконец, если особая точка c удовлетворяет условию a<c<b, то интеграл определяется так
 . .
Заметьте, что 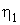 и и 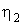 разные. Если взять их одинаковыми, то
получающийся предел разные. Если взять их одинаковыми, то
получающийся предел
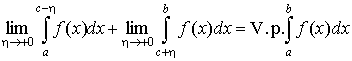
называется главным значением несобственного
интеграла второго рода.
6.5 Признаки
существования несобственных интегралов второго рода от неотрицательных функций
В этом разделе всюду предполагается,
что  и и 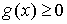 . .
Теорема
1. Если 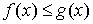 , то , то
1. если 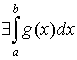 , то , то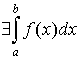 ; ;
2. если 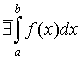 , то , то 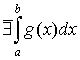 . .
Теорема
2. Пусть b есть
особая точка функции f(x). Если
при x®b существует предел
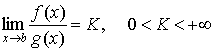 , ,
то интегралы 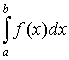 и и  сходятся или
расходятся одновременно. сходятся или
расходятся одновременно.
Практический
признак сходимости.
Пусть b есть особая точка функции f(x). Если при x®b существует предел
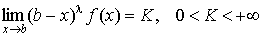 , ,
то при 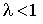 интеграл интеграл 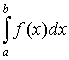 сходится; сходится;
при 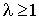 интеграл интеграл 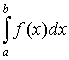 расходится. расходится.
Если особой точкой является точка а, то предел принимает вид
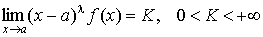 . .
|