4. ПОСТРОЕНИЕ МОДЕЛЕЙ ТРАНСПОРТНОЙ ЗАДАЧИ
4.1. Теоретическое введение
Задача о размещении (транспортная задача) – это РЗ, в
которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах
ресурсы могут быть разделены между работами, и отдельные работы могут быть
выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является
распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.
Стандартная ТЗ определяется как задача разработки наиболее экономичного
плана перевозки продукции одного вида из нескольких пунктов
отправления в пункты назначения. При этом величина транспортных расходов прямо
пропорциональна объему перевозимой продукции и задается с помощью тарифов на
перевозку единицы продукции.
Исходные
параметры модели ТЗ
1)
n –
количество пунктов отправления, m –
количество пунктов назначения.
2)
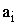 – запас продукции в пункте отправления
– запас продукции в пункте отправления 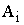 (
(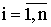 ) [ед. прод.].
) [ед. прод.].
3)
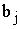 – спрос на продукцию в пункте назначения
– спрос на продукцию в пункте назначения 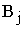 (
(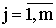 ) [ед. прод.].
) [ед. прод.].
4)
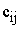 – тариф (стоимость) перевозки единицы продукции из
пункта отправления
– тариф (стоимость) перевозки единицы продукции из
пункта отправления 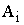 в пункт назначения
в пункт назначения 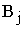 [руб./ед. прод.].
[руб./ед. прод.].
Искомые
параметры модели ТЗ
1)
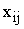 – количество продукции, перевозимой из пункта отправления
– количество продукции, перевозимой из пункта отправления
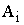 в пункт назначения
в пункт назначения 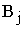 [ед. прод.].
[ед. прод.].
2)
 – транспортные расходы на перевозку всей продукции
[руб.].
– транспортные расходы на перевозку всей продукции
[руб.].
Этапы построения модели
I.
Определение переменных.
II.
Проверка сбалансированности задачи.
III.
Построение сбалансированной транспортной матрицы.
IV.
Задание ЦФ.
V.
Задание ограничений.
Транспортная
модель
|
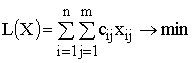 ; ;
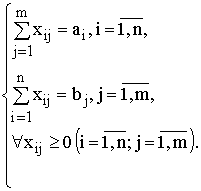
|
(4.1)
|
ЦФ представляет собой общие транспортные расходы на осуществление всех
перевозок в целом. Первая группа ограничений указывает, что запас продукции в
любом пункте отправления должен быть равен суммарному объему перевозок
продукции из этого пункта. Вторая группа ограничений указывает, что суммарные
перевозки продукции в некоторый пункт потребления должны полностью
удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления
модели ТЗ является транспортная матрица (табл. 4.1).
Таблица
4.1
Общий
вид транспортной матрицы
|
Пункты
отправления, 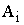
|
Пункты потребления,
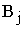
|
Запасы,
ед. прод.
|
|
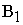
|
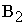
|
…
|
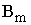
|
|
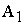
|
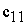 , [руб./ед. прод.] , [руб./ед. прод.]
|
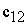
|
…
|
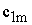
|
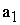
|
|
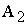
|
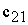
|
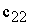
|
…
|
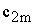
|
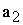
|
|
…
|
…
|
…
|
…
|
…
|
…
|
|
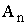
|
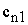
|
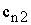
|
…
|
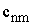
|
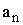
|
|
Потребность
ед. прод.
|
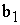
|
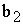
|
…
|
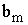
|
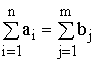
|
Из модели (4.1) следует, что сумма запасов продукции во всех
пунктах отправления должна равняться суммарной потребности во всех пунктах потребления,
т.е.
|
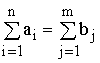 . .
|
(4.2)
|
Если (4.2) выполняется, то ТЗ называется сбалансированной (закрытой),
в противном случае – несбалансированной
(открытой). В случае, когда суммарные
запасы превышают суммарные потребности, необходим дополнительный фиктивный (реально не существующий)
пункт потребления, который будет формально потреблять существующий излишек
запасов, т.е.
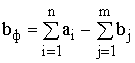 .
.
Если суммарные
потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально
восполняющий существующий недостаток продукции в пунктах отправления:
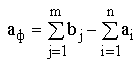 .
.
Для фиктивных перевозок вводятся фиктивные
тарифы 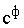 , величина которых обычно приравнивается к нулю
, величина которых обычно приравнивается к нулю 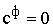 . Но в некоторых ситуациях величину фиктивного тарифа можно
интерпретировать как штраф, которым облагается каждая единица
недопоставленной продукции. В этом случае величина
. Но в некоторых ситуациях величину фиктивного тарифа можно
интерпретировать как штраф, которым облагается каждая единица
недопоставленной продукции. В этом случае величина 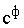 может быть любым
положительным числом.
может быть любым
положительным числом.
Задача о назначениях – частный случай ТЗ. В задаче о
назначениях количество пунктов отправления равно количеству пунктов назначения.
Объемы потребности и предложения в каждом из пунктов назначения и отправления
равны 1. Примером типичной задачи о назначениях является распределение
работников по различным видам работ, минимизирующее суммарное время выполнения
работ.
Переменные задачи о
назначениях определяются следующим
образом

4.2. Методические рекомендации
4.2.1. Стандартная транспортная задача
Задача №4.01
Заводы некоторой автомобильной фирмы расположены в городах А, В и С.
Основные центры распределения продукции сосредоточены в городах D и E. Объемы
производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей
ежеквартально. Величины квартального спроса в центрах распределения составляют
2300 и 1400 автомобилей соответственно. Стоимости перевозки автомобилей по
железной дороге по каждому из возможных маршрутов приведены в табл.4.2.
Таблица 4.2
Стоимость перевозки автомобилей, руб./шт.
|
|
D
|
E
|
|
А
|
80
|
215
|
|
В
|
100
|
108
|
|
С
|
102
|
68
|
Постройте математическую модель, позволяющую определить количество
автомобилей, перевозимых из каждого завода в каждый центр распределения, таким
образом, чтобы общие транспортные расходы были минимальны.
Решение
Определение переменных
Обозначим количество автомобилей, перевозимых из i-го завода в j-й пункт
потребления через 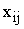 .
.
Проверка сбалансированности задачи
Проверим равенство суммарного производства автомобилей и суммарного
спроса
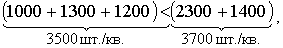
откуда следует
вывод – задача несбалансирована, поскольку спрос на автомобили превышает
объем их производства. Для установления баланса введем дополнительный фиктивный завод с ежеквартальным объемом производства 200 шт. (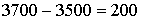 ). Фиктивные тарифы
). Фиктивные тарифы 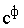 приравняем к нулю
(т.к. перевозки в действительности производиться не будут).
приравняем к нулю
(т.к. перевозки в действительности производиться не будут).
Построение транспортной матрицы
Согласно результатам проверки сбалансированности задачи №4.01 в
транспортной матрице должно быть четыре строки, соответствующих заводам и два
столбца, соответствующих центрам распределения (см. табл.4.3). Тариф перевозки
обычно вписывают в правом нижнем углу клетки матрицы для удобства
дальнейшего нахождения опорных планов задачи.
Таблица 4.3
Транспортная матрица задачи №4.01
|
|
D
|
E
|
Объем произв.,
шт./квартал
|
|
А
|
|
|
|
|
1000
|
|
|
80
|
|
215
|
|
B
|
|
|
|
|
1300
|
|
|
100
|
|
108
|
|
C
|
|
|
|
|
1200
|
|
|
102
|
|
68
|
|
Фиктивный завод
|
|
|
|
|
200
|
|
|
0
|
|
0
|
|
Спрос, шт./квартал
|
2300
|
1400
|
3700
|
Задание ЦФ
Суммарные
затраты в рублях на ежеквартальную перевозку автомобилей определяются по
формуле
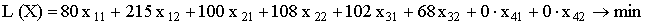
Задание ограничений
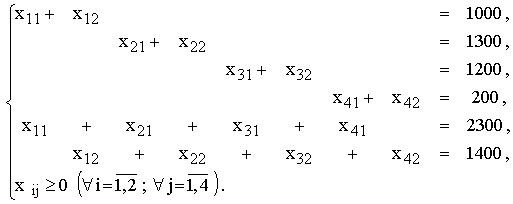 [шт./квартал]
[шт./квартал]
4.2.2. Модификации стандартной транспортной задачи
Недопустимые перевозки
Иногда в определенных направлениях перевозки продукции невозможны,
например, по причине ремонта транспортных магистралей. Такие ситуации моделируются
с помощью введения так называемых запрещающих
тарифов 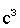 . Запрещающие тарифы должны сделать невыгодными перевозки в
соответствующих направлениях. Для этого величина запрещающих тарифов должна
быть больше реальных тарифов в транспортной матрице
. Запрещающие тарифы должны сделать невыгодными перевозки в
соответствующих направлениях. Для этого величина запрещающих тарифов должна
быть больше реальных тарифов в транспортной матрице
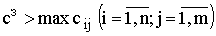 .
.
Максимизация
ЦФ
Существующий алгоритм решения транспортных задач (метод потенциалов)
предполагает, что ЦФ стремится к минимуму. Однако существуют ситуации, когда в
рамках транспортной модели требуется максимизировать ЦФ, например, общий доход,
объем продаж, прибыль, качество выполняемых работ и т.д. В этом случае в модель
вместо искомой ЦФ  вводится ЦФ
вводится ЦФ 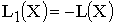 , в которой тарифы умножаются на (-1). Таким образом,
максимизация
, в которой тарифы умножаются на (-1). Таким образом,
максимизация  будет соответствовать
минимизации
будет соответствовать
минимизации 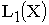 .
.
Многопродуктовые модели
Если в задаче идет речь о том, что из каждого пункта отправления можно
перевозить продукцию нескольких видов, то при построении модели можно использовать
один из следующих вариантов:
·
каждому виду продукции должна соответствовать
одна транспортная матрица;
·
все виды продукции представлены в одной общей
матрице с использованием запрещающих тарифов в клетках, связывающих разные виды
продукции.