|
Лекция
7
Определение паросочений в
графе и их разновидностей. Двудольные графы и алгоритм выбора наибольшего
паросочетания в двудольном графе. Решение задачи о назначениях на узкие места.
Пусть 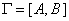 - граф и - граф и 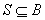 - некоторое множество
ребер в нем. Множество - некоторое множество
ребер в нем. Множество 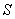 называется паросочетанием, если любые два ребра из
него не имеют общей вершины. Договоримся, что множество из одного ребра тоже
будет называться паросочетанием, как
и всякое пустое множество. называется паросочетанием, если любые два ребра из
него не имеют общей вершины. Договоримся, что множество из одного ребра тоже
будет называться паросочетанием, как
и всякое пустое множество.
Паросочетание называется максимальным, если к нему нельзя
добавить ни одного ребра так, чтобы снова получилось паросочетание. Наконец,
паросочетание называется наибольшим,
если оно состоит из наибольшего возможного количества ребер. Очевидно, каждое
наибольшее паросочетание является максимальным; обратное неверно - вот пример:
здесь красные
ребра - максимальное, но не наибольшее паросочетание, а черные ребра –
паросочетание наибольшее.
Поиск наибольшего паросочетания в
графе представляет собой классическую алгоритмическую задачу. Мы рассмотрим ее
решение не для общего случая, а для графов частного вида - графов двудольных. Граф 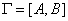 называется двудольным, если его множество вершин A
можно представить в виде
объединения двух его непустых подмножеств называется двудольным, если его множество вершин A
можно представить в виде
объединения двух его непустых подмножеств 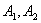 без общих элементов
так, что любое ребро из B
будет иметь один конец в без общих элементов
так, что любое ребро из B
будет иметь один конец в 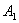 , а другой конец - в , а другой конец - в 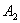 . Таким образом, нет ни одного ребра, которое соединяло бы
вершины из . Таким образом, нет ни одного ребра, которое соединяло бы
вершины из 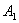 или соединяло бы
вершины из или соединяло бы
вершины из 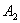 . .
Если считать, что 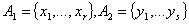 , то двудольный граф можно описать не только известной уже
матрицей смежностей, но и следующей матрицей
двудольного графа: эта матрица – размером , то двудольный граф можно описать не только известной уже
матрицей смежностей, но и следующей матрицей
двудольного графа: эта матрица – размером 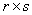 и, если обозначать ее
общий элемент через и, если обозначать ее
общий элемент через 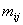 , то полагают , то полагают
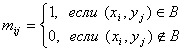 . .
Ясно, что такая
матрица описывает граф однозначно, хотя является намного меньшей по объему, чем
матрица смежностей графа в этом случае.
Когда множество 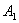 состоит из состоит из 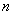 вершин, а множество вершин, а множество 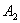 состоит из состоит из 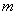 вершин и в двудольном
графе проведены все возможные ребра,
то говорят, что двудольный граф вершин и в двудольном
графе проведены все возможные ребра,
то говорят, что двудольный граф 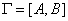 является полным двудольным графом и обозначают
его символом является полным двудольным графом и обозначают
его символом 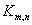 . .
Мы опишем сейчас алгоритм выбора
наибольшего сочетания в двудольном графе, опираясь на только что введенное
понятие матрицы двудольного графа.
Шаг 0. По матрице 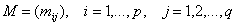 данного двудольного
графа строим рабочую таблицу: она представляет собой матрицу тех же размеров; в
клетку с номером данного двудольного
графа строим рабочую таблицу: она представляет собой матрицу тех же размеров; в
клетку с номером 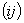 поместим символ «´» и назовем ее недопустимой, если в матрице двудольного графа поместим символ «´» и назовем ее недопустимой, если в матрице двудольного графа 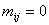 ; если же ; если же 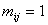 , то в клетку рабочей таблицы не запишем ничего и назовем такую
клетку допустимой. Слева от рабочей
таблицы расположим для удобства номера ее строк, а сверху над таблицей
расположим номера ее столбцов. Шаг 1. Просмотрим слева направо первую строку и в
первую же допустимую клетку первой строки поставим символ «1». Если в первой
строке все клетки недопустимы, то перейдем ко второй строке и в первую же (при
просмотре слева направо) допустимую клетку поставим «1». Если же нет допустимых
клеток и во второй строке, то проставим указанным выше способом «1» в третьей
строке. Если окажется, что во всей таблице все клетки недопустимы, то на этом
все действия заканчиваются и выдается ответ: «в графе нет ребер». Если же
все-таки удастся поставить первую «1», то после этого просмотрим все остальные
строки таблицы в порядке возрастания их номеров. В каждой очередной строке
просматриваем ее клетки слева на-право и фиксируем первую по ходу просмотра
допустимую клетку такую, которая является не-зависимой по отношению к
допустимым клеткам, в которых уже стоит символ «1», и проставляем в эту клетку
«1», после чего переходим к тем же действиям в следующей строке. Если в строке
такой клетки не окажется, то переходим к следующей строке и выполняем в ней ту
же проверку. , то в клетку рабочей таблицы не запишем ничего и назовем такую
клетку допустимой. Слева от рабочей
таблицы расположим для удобства номера ее строк, а сверху над таблицей
расположим номера ее столбцов. Шаг 1. Просмотрим слева направо первую строку и в
первую же допустимую клетку первой строки поставим символ «1». Если в первой
строке все клетки недопустимы, то перейдем ко второй строке и в первую же (при
просмотре слева направо) допустимую клетку поставим «1». Если же нет допустимых
клеток и во второй строке, то проставим указанным выше способом «1» в третьей
строке. Если окажется, что во всей таблице все клетки недопустимы, то на этом
все действия заканчиваются и выдается ответ: «в графе нет ребер». Если же
все-таки удастся поставить первую «1», то после этого просмотрим все остальные
строки таблицы в порядке возрастания их номеров. В каждой очередной строке
просматриваем ее клетки слева на-право и фиксируем первую по ходу просмотра
допустимую клетку такую, которая является не-зависимой по отношению к
допустимым клеткам, в которых уже стоит символ «1», и проставляем в эту клетку
«1», после чего переходим к тем же действиям в следующей строке. Если в строке
такой клетки не окажется, то переходим к следующей строке и выполняем в ней ту
же проверку.
Фиксируем набор ребер в графе,
соответствующих проставленным в таблице символам «1». (Под ребром, соответствующим символу «1» в рабочей
таблице, подразумевается следующее: если «1» стоит в клетке с номером 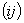 , то соответствующим
будет ребро , то соответствующим
будет ребро 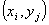 .) Легко заметить, что этот набор ребер - максимальное
паросочетание. .) Легко заметить, что этот набор ребер - максимальное
паросочетание.
Если в результате проведения всех
действий на этом шагу в каждой строке рабочей таблицы окажется символ «1», то
ребра из указанного только что паросочетания и составляют наибольшее
паросочетание, и действия окончены. Если же в результате проведения первого
шага остались строки без «1», то пометим их справа от таблицы символом «-»
переходим к следующему шагу.
Шаг 2. Просмотрим все
помеченные строки в порядке возрастания их номеров. Просмотр очередной строки
состоит в следующем: в строке отыскиваются допустимые клетки, и столбцы, в
которых эти клетки расположены, помечаются номером просматриваемой строки. При
этом соблюдается принцип (Ã): если пометка уже стоит, то на ее место
вторая не ставится. Пометки, о которых только что было сказано, физически
выставляются внизу, под таблицей.
Если в результате этого шага ни один
из столбцов не будет помечен, то это означает, что уже имеющееся паросочетание
(полученное на Шаге 1) является искомым наибольшим и все действия
прекращаются. Если же среди столбцов появятся помеченные, то переходим к
следующему шагу.
Шаг 3. Просмотрим помеченные
столбцы в порядке возрастания их номеров. Просмотр столбца состоит в следующем:
в столбце отыскивается символ «1» и строка, в которой он расположен, помечается
номером просматриваемого столбца.
Физически пометки выставляются
справа от таблицы, на уровне соответствующих строк. Всегда соблюдается принцип
(Ã).
Если в результате действий по этому
шагу возникнет ситуация, когда в просматриваемом столбце нет символа «1», то
действия на данном шагу прерываются и надо перейти к следующему шагу - Шагу
4. Если же в результате действий по
этому шагу будут просмотрены все помеченные ранее столбцы и, тем самым,
возникнет набор помеченных строк (одни будут помечены символом «-», другие -
номерами столбцов), то следует вернуться к Шагу 2 и повторить
предусмотренные им действия.
Если в результате этих действий по Шагу
2 не возникнет новых помеченных столбцов, то это означает, что имеющееся
паросочетание является искомым и процесс останавливается. Если же среди
помечаемых столбцов возникнут новые помеченные столбцы, то следует повторить Шаг
3 с новым набором помеченных столбцов. Если в результате этих действий не
возникнет новых помеченных строк, то это означает, что имеющееся паросочетание
является искомым.
Шаг 4. Рассматривается
столбец, имеющий пометку и не содержащий символа «1». Мы сейчас изменим набор
символов «1», расположенных в рабочей таблице.
В рассматриваемый столбец поставим
символ «1» в строку, номер которой равен пометке этого столбца. Затем в этой
строке отыщем «старый» символ «1» и переместим его по его столбцу в строку,
номер которой равен пометке при этом столбце. (Можно доказать, что описанное
действие реально всегда осуществимо.) Затем в строке, куда попал последний
символ «1» отыщем «старый» символ «1» и с ним проделаем то же самое. В конце
концов очередной перемещаемый «старый» символ «1» окажется в строке, где больше
символов «1» нет. Возник новый набор символов «1», в котором уже элементов на
один больше, чем в исходном наборе символов «1». По этому новому набору можно
построить паросочетание так же, как это делалось в самом начале и после этого
повторить все сначала.
В конце концов возникнет одно из
указанных выше условий прекращения действий по алгоритму и наибольшее
паросочетание будет найдено.
Рассмотрим пример. Найти наибольшее
паросочетание в следующем двудольном графе со следующей матрицей:
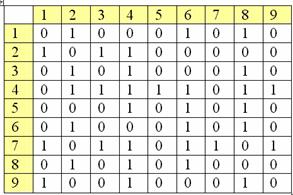
Сам двудольный
граф в этом примере выглядит так:
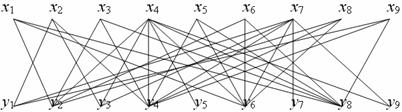
Будем
проводить шаг за шагом описанный выше алгоритм. Рабочая таблица:
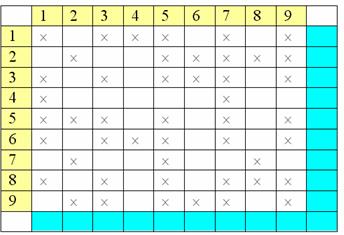
Выполняем первый
шаг: расставляем независимые единицы и отмечаем строки, в которые единицы не
попали:
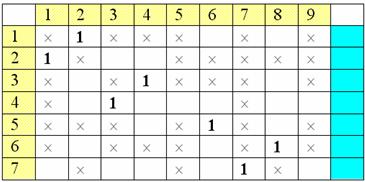
Паросочетание,
которое соответствует выбранным единицам:
.
Далее столбцы
допустимых клеток помеченных строк пометим номерами этих строк, следуя принципу
(Ã):
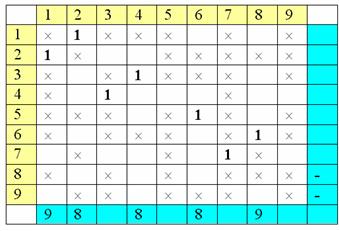
Далее в
помеченных столбцах отыщем единицы и их строки пометим номерами их столбцов:
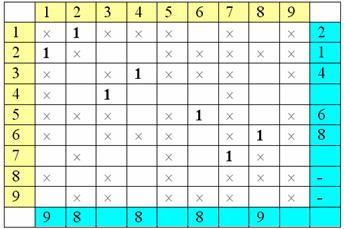
Теперь снова
пометим столбцы, отправляясь от помеченных строк и соблюдая принцип (Ã):
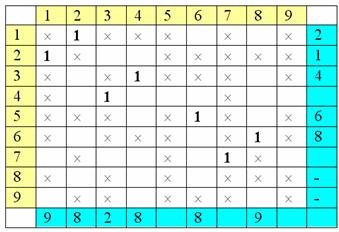
Теперь снова просмотрим
помеченные столбцы и пометим строки:
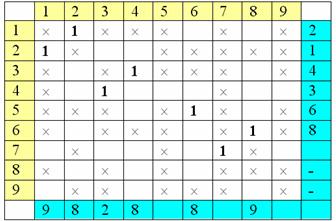
Теперь снова
пометим столбцы (при принципе (Ã)):
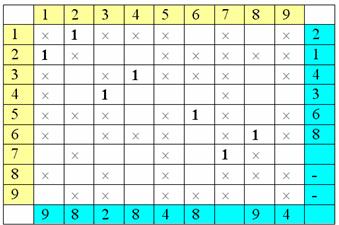
Теперь - снова
строки:
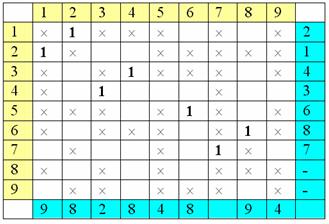
Сложилась
ситуация, когда в столбце №9 с пометкой «4» нет единицы. Следовательно, можно
набор единиц можно увеличить на одну
(старые единицы
остаются черными, новые - красные):
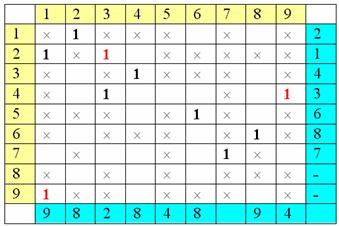
Мы получили
новый набор независимых единиц:
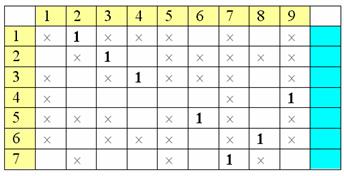
Теперь вся процедура повторяется
сначала, и на последней таблице уже указана единственная пометка «-» у строки
№8. Пометим столбцы допустимых клеток этой строки ее номером:
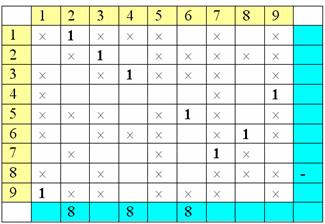
Затем в
помеченных столбцах найдем единицы и их строки пометим
номерами
столбцов:
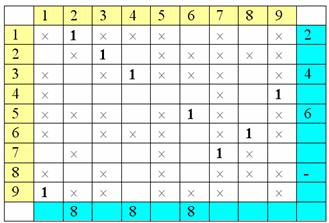
Затем столбцы
допустимых клеток помеченных строк:
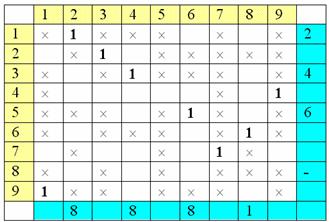
Затем снова
строки:
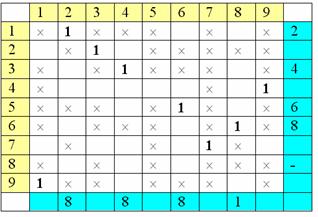
Затем снова
столбцы:
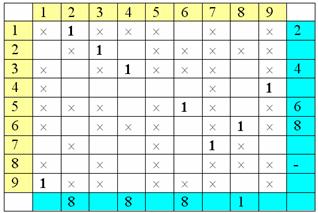
Сложилась ситуация, когда расстановка
пометок «зациклилась». Это означает, что искомое паросочетание состоит из
ребер, соответствующих проставленным единицам.
В заключение рассмотрим задачу о назначении на узкие места, которая
решается описанным выше алгоритмом. Вот ее постановка.
Имеется 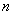 рабочих мест рабочих мест 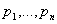 на некотором конвейере
и на некотором конвейере
и 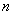 рабочих рабочих 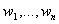 , кото-рых нужно на эти рабочие места расставить; известна
производительность , кото-рых нужно на эти рабочие места расставить; известна
производительность 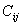 рабочего рабочего 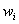 на рабочем месте на рабочем месте 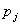 . Тот факт, что при некотором распределении на рабочие места
рабочий . Тот факт, что при некотором распределении на рабочие места
рабочий 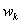 попадает на рабочее
место попадает на рабочее
место 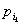 можно описать
следующей таблицей: можно описать
следующей таблицей:
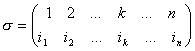 . .
Имея способ s
назначения на рабочие места, можно найти конкретную для этого способа
минимальную производительность 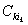 и заметить, что именно
эта минимальная производительность и определяет скорость и производительность
конвейера. То рабочее место, на котором реализуется минимальная
производительность и называют узким
местом в назначении. и заметить, что именно
эта минимальная производительность и определяет скорость и производительность
конвейера. То рабочее место, на котором реализуется минимальная
производительность и называют узким
местом в назначении.
Приведем алгоритм решения задачи о
назначении на узкие места.
Шаг 0. Фиксируем матрицу
производительностей 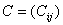 и любое назначение на рабочие
места (например, рабочий и любое назначение на рабочие
места (например, рабочий 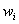 назначается на рабочее
место назначается на рабочее
место 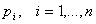 ). Пусть ). Пусть 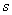 - минимальная
производительность при этом назначении. Построим рабочую таблицу тех же - минимальная
производительность при этом назначении. Построим рабочую таблицу тех же
размеров, что и
матрица 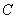 ; в клетку с номером ; в клетку с номером 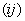 в этой таблице
проставим символ «´», если в этой таблице
проставим символ «´», если 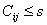 ; в противном случае эту клетку оставим пустой. ; в противном случае эту клетку оставим пустой.
Шаг 1. Рассматривая рабочую
таблицу, построенную на предыдущем шагу, как рабочую таблицу в алгоритме для
выбора наибольшего паросочетания в двудольном графе, найдем соответствующее
наибольшее паросочетание. Если в нем окажется 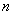 ребер, то по ним
восстанавливается новое назначение на рабочие места и с новой, более высокой,
минимальной производительностью. Обозначим ее снова через ребер, то по ним
восстанавливается новое назначение на рабочие места и с новой, более высокой,
минимальной производительностью. Обозначим ее снова через 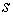 и вернемся к Шагу 0.
Если же число ребер окажется меньше и вернемся к Шагу 0.
Если же число ребер окажется меньше 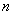 , то имеющееся назначение на рабочие места уже оптимально. , то имеющееся назначение на рабочие места уже оптимально.
Лекция
8
Цепи и антицепи в
частично-упорядоченном множестве. Теорема Дилворта. Алгоритм разбиения
частично-упорядоченного множества на минимальное число цепей.
Пусть 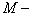 частично упорядоченное
множество (сокращенно: ЧУМ). Это значит, что задано некоторое подмножество частично упорядоченное
множество (сокращенно: ЧУМ). Это значит, что задано некоторое подмножество 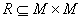 такое, что выполнены следующие условия: для всякого такое, что выполнены следующие условия: для всякого 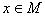 обязательно обязательно 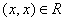 (это, так называемая, рефлексивность); если (это, так называемая, рефлексивность); если 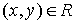 и и 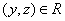 , то обязательно , то обязательно 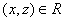 (это, так называемая, транзитивность); если (это, так называемая, транзитивность); если 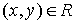 и и 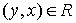 , то обязательно , то обязательно 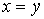 (это, так называемая, антисимметричность). Само множество (это, так называемая, антисимметричность). Само множество 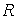 называется частичным порядком. На одном и том же
множестве называется частичным порядком. На одном и том же
множестве 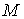 может быть много
частичных порядков. может быть много
частичных порядков.
Если частичный порядок 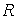 таков, что для любых
двух элементов таков, что для любых
двух элементов 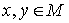 либо либо 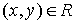 либо либо 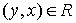 , то говорят, что множество , то говорят, что множество 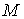 является цепью;
если же частичный порядок является цепью;
если же частичный порядок 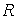 таков, что для любых
различных таков, что для любых
различных 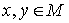 ни одно из включений - ни одно из включений -
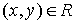 , , 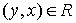 - не выполняется, то
говорят, что - не выполняется, то
говорят, что 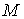 является антицепью. Очевидно, что если является антицепью. Очевидно, что если 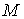 - ЧУМ, то и любое
подмножество в - ЧУМ, то и любое
подмножество в 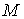 является
частично-упорядоченным. По определению полагают, что всякое одноэлементное
подмножество является одновременно и цепью и антицепью. является
частично-упорядоченным. По определению полагают, что всякое одноэлементное
подмножество является одновременно и цепью и антицепью.
Рассмотрим пример. Пусть 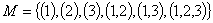 (это означает, что
элемента-ми множества (это означает, что
элемента-ми множества 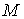 являются наборы
указанных натуральных чисел). Определим частичный порядок являются наборы
указанных натуральных чисел). Определим частичный порядок 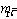 , объявив, что , объявив, что 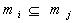 , если , если 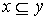 . Нетрудно проверить, что это - действительно частичный
порядок. В этом частичном порядке . Нетрудно проверить, что это - действительно частичный
порядок. В этом частичном порядке 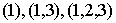 - цепь, а - цепь, а 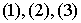 - антицепь. - антицепь.
Существует классическая задача: разбить ЧУМ 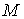 на минимальное число цепей. Это значит надо найти в на минимальное число цепей. Это значит надо найти в 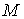 цепи цепи 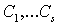 такие, что у любых
двух из них нет общих элементов, что их объединение совпадает с такие, что у любых
двух из них нет общих элементов, что их объединение совпадает с 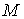 и при всем при этом
число и при всем при этом
число 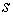 минимально возможное.
Имеется по этому поводу классическая теорема
Дилворта, утверждающая следующее: минимально возможное.
Имеется по этому поводу классическая теорема
Дилворта, утверждающая следующее:
минимальное
число цепей, на которые можно разбить данное частично упорядоченное множество,
равно максимальному числу элементов, составляющих антицепь.
Мы приведем сейчас алгоритм,
позволяющий отыскать одно из возможных минимальных
цепных разбиений ЧУМа, т.е. найти набор попарно неперсекающихся цепей 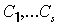 , объединение которых совпадает с , объединение которых совпадает с 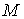 и при этом и при этом 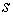 минимально возможное. минимально возможное.
Для удобства мы будем в будущем
выражать тот факт, что 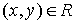 в ЧУМе в ЧУМе 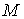 символом символом 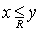 или просто или просто 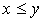 , причем если к тому же , причем если к тому же 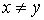 , то будем писать , то будем писать 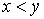 . .
Итак, пусть 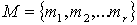 - ЧУМ; требуется найти
минимальное цепное разбиение. - ЧУМ; требуется найти
минимальное цепное разбиение.
Шаг 0. Построим двудольный
граф 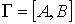 следующим образом.
Положим следующим образом.
Положим 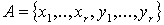 ; это означает, что в графе будет ровно ; это означает, что в графе будет ровно 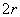 вершин. Далее, ребра в
графе будут иметь лишь следующий вид: вершин. Далее, ребра в
графе будут иметь лишь следующий вид: 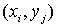 , причем , причем 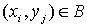 тогда и только тогда,
когда тогда и только тогда,
когда 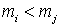 . .
Шаг 1. Выберем в построенном
графе G наибольшее паросочетание 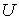 . Для каждого ребра . Для каждого ребра 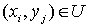 фиксируем пару
элементов фиксируем пару
элементов 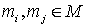 , составляющих, естественно, цепь, так как по определению
ребер в G обязательно , составляющих, естественно, цепь, так как по определению
ребер в G обязательно 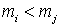 . .
Шаг 2. Многократно используя
свойство транзитивности частичного порядка, объединим двухэлементные цепи из
предыдущего шага в неудлиняемые цепи. В результате получится некоторый набор
цепей 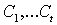 в данном множестве,
причем, как нетрудно проверить, эти цепи попарно общих элементов не имеют.
Добавив к этому списку цепей одноэлементные цепи, полученные из всех элементов
данного множества, не вошедших в объединение в данном множестве,
причем, как нетрудно проверить, эти цепи попарно общих элементов не имеют.
Добавив к этому списку цепей одноэлементные цепи, полученные из всех элементов
данного множества, не вошедших в объединение 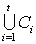 , мы получим некоторое цепное разбиение данного множества , мы получим некоторое цепное разбиение данного множества 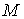 . Можно доказать, что это
цепное разбиение минимально. . Можно доказать, что это
цепное разбиение минимально.
ПРИМЕР. Пусть множество 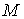 состоит из следующих
наборов чисел (каждый набор заключен в круглые скобки): состоит из следующих
наборов чисел (каждый набор заключен в круглые скобки):
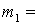 Æ (пустое
множество; это - тоже элемент из Æ (пустое
множество; это - тоже элемент из 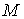 ); );
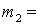 (1), (1), 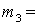 (2), (2), 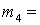 (3), (3), 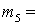 (4), (4), 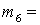 (1,2), (1,2), 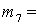 (1,3), (1,3), 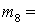 (1,4), (1,4), 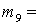 (2,3), (2,3), 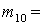 (2,4), (2,4), 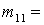 (3,4), (3,4), 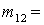 (1,2,3), (1,2,3), 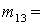 (1,2,4), (1,2,4), 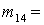 (1,3,4), (1,3,4), 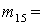 (2,3,4), (2,3,4), 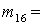 (1,2,3,4). (1,2,3,4).
Частичный порядок на 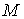 будет считаться по
включению: будет считаться по
включению: 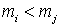 тогда и только тогда,
когда тогда и только тогда,
когда 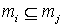 . .
Найдем минимальное цепное разбиение
этого множества. Вначале построим двудольный граф для данной задачи. Вот его
матрица:
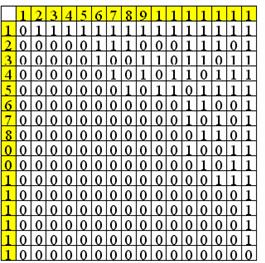
Найдем
наибольшее паросочетание:
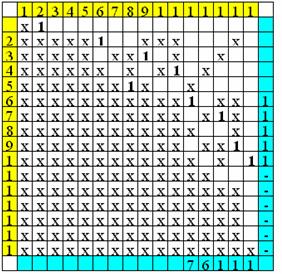
Следовательно,
наибольшее паросочетание таково:
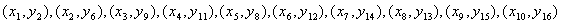 . .
Отсюда - первые
«двухэлементные цепочки»:
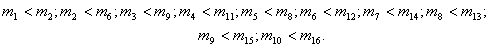
Используя
транзитивность частичного порядка, склеим некоторые из этих цепочек:
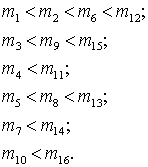
Поскольку не осталось элементов
данного множества вне указанных цепей, этот набор цепей и является минимальным
цепным разбиением.
|