|
Лекция
9
Планарные и плоские графы.
Формулировки теоремы Понтрягина-Куратовского и теоремы Эйлера о соотношении
чисел граней, ребер и вершин плоского графа.
Граф 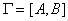 называется планарным, если хотя бы одна из его
геометрических интерпретаций такова, что ребра графа пересекаются только в его
вершинах. Например, граф называется планарным, если хотя бы одна из его
геометрических интерпретаций такова, что ребра графа пересекаются только в его
вершинах. Например, граф
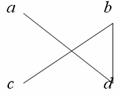
планарен, потому
что его можно изобразить и так:

Планарный граф,
уже изображенный на плоскости в таком виде, что его ребра пересекаются только в
его вершинах, называется плоским.
Таким образом, последний из изображенных выше графов является плоским, а первый
- нет.
В математике доказывается, что не являются планарными два следующих графа:
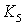 (полный граф на пяти
вершинах) и (полный граф на пяти
вершинах) и 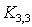 (полный двудольный граф, каждая доля в котором
состоит из трех вершин). Существует классическая теорема Понтрягина-Куратовского, которая утверждает следующее: граф планарен тогда и только тогда, когда в
нем нет подграфов, полученных подразбиением ребер из (полный двудольный граф, каждая доля в котором
состоит из трех вершин). Существует классическая теорема Понтрягина-Куратовского, которая утверждает следующее: граф планарен тогда и только тогда, когда в
нем нет подграфов, полученных подразбиением ребер из 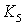 и и 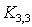 . .
Опишем классическую конструкцию
Эйлера, связанную с плоскими графами.
Пусть  - плоский граф. Это
означает, что имеется определенное изображение его на плоскости, в котором ребра
пересекаются только в вершинах. Каждый простой цикл такого графа ограничивает
две части плоскости: одна - внутренняя (ограниченная), другая - внешняя
(неограниченная). Если по части плоскости, ограниченной простым циклом плоского
графа, не проходит ни одна цепь этого графа, начало и конец которой принадлежат
обсуждаемому циклу, то эта часть плоскости называется гранью плоского графа. Если грань неограниченная, то она называется
внешней; ограниченная грань плоского
графа называется внутренней. - плоский граф. Это
означает, что имеется определенное изображение его на плоскости, в котором ребра
пересекаются только в вершинах. Каждый простой цикл такого графа ограничивает
две части плоскости: одна - внутренняя (ограниченная), другая - внешняя
(неограниченная). Если по части плоскости, ограниченной простым циклом плоского
графа, не проходит ни одна цепь этого графа, начало и конец которой принадлежат
обсуждаемому циклу, то эта часть плоскости называется гранью плоского графа. Если грань неограниченная, то она называется
внешней; ограниченная грань плоского
графа называется внутренней.
Можно
доказать, что у каждого плоского графа
обязательно есть внешняя грань и притом
только одна.
Подсчитаем
для примера количество граней в каком-нибудь плоском графе. Пусть имеется
следующий плоский граф:
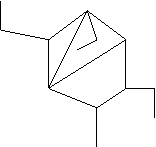
Здесь - четыре грани, причем одна из них
- внешняя. Заметим, кстати, что здесь вершин - 13, а ребер - 15. Подсчитаем те же параметры
(количества граней, вершин и ребер еще в
одном примере:
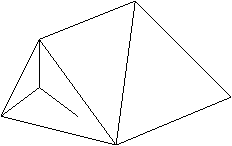
Здесь граней - 5, вершин - 7, ребер - 10.
Классическая
теорема Эйлера утверждает: если в плоском графе имеется «г» граней, «в»
вершин
и «р» ребер, то обязательно выполняется равенство: «г» +
«в» - «р»=2.
Отсюда
возникает множество соотношений для плоских графов, из которых остановимся только на одном, Фиксируем какой-нибудь
плоский граф. Пусть в нем 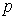 вершин и вершин и 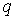 ребер. К этому графу можно, при необходимости,
добавить ребра и получить снова плоский граф с тем же количеством вершин, но с увеличенным
количеством ребер такой, что все грани в нем будут ограниченны треугольниками (включая
внешнюю). Если ребер. К этому графу можно, при необходимости,
добавить ребра и получить снова плоский граф с тем же количеством вершин, но с увеличенным
количеством ребер такой, что все грани в нем будут ограниченны треугольниками (включая
внешнюю). Если 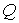 - новое количество
ребер и - новое количество
ребер и 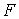 - количество граней в
этом новом графе, то - количество граней в
этом новом графе, то 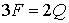 ; тогда теорема Эйлера приобретает вид: ; тогда теорема Эйлера приобретает вид: 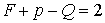 , но , но 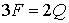 , так что , так что 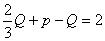 , откуда , откуда 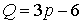 , а для произвольного
плоского графа,
следовательно, , а для произвольного
плоского графа,
следовательно,
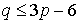 . .
Лекция 10
Раскраска
графа. Формулировка теоремы о пяти красках. Хроматическое число и алгоритм
Зыкова вычисления хроматического многочлена графа.
Пусть 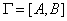 и и  - любая функция на
множестве вершин с натуральными значениями. Такая функция называется раскраской, если ее значения на любых
двух смежных вершинах различны; значения раскраски, как функции, называются цветами, так что относи- тельно любой
раскраски смежные вершины являются «разноцветными». - любая функция на
множестве вершин с натуральными значениями. Такая функция называется раскраской, если ее значения на любых
двух смежных вершинах различны; значения раскраски, как функции, называются цветами, так что относи- тельно любой
раскраски смежные вершины являются «разноцветными».
Существует давняя задача о поиске
минимального числа цветов, которыми можно раскрасить данный граф. В принципе,
осуществить такую раскраску данного графа можно прямым перебором возможных
ситуаций по следующей схеме.
Заметим, что если 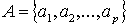 , то всякая функция на , то всякая функция на 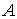 с натуральными
значениями - это таблица вида с натуральными
значениями - это таблица вида
|
A
|
a1
|
a2
|
...
|
ap
|
|
f(A)
|
n1
|
n2
|
...
|
np
|
здесь в первой
строчке перечислены вершины графа, а во второй те натуральные числа, которые
данная функция вершинам сопоставляет. Очевидно, достаточно рассматривать те
ситуации, в которых все 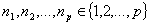 . Следовательно, общее количество функций вида . Следовательно, общее количество функций вида
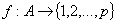 вполне вычисляемо -
это вполне вычисляемо -
это 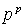 . Часть этих функций - раскраски, часть - нет. Проверить,
является ли данная функция раскраской или нет, можно перебирая все ребра из . Часть этих функций - раскраски, часть - нет. Проверить,
является ли данная функция раскраской или нет, можно перебирая все ребра из 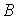 : выясняется, одинаковы ли значения функции на концах ребер.
Имея полный список раскрасок, можно найти среди них такие, для которых
количество значений функции минимально. : выясняется, одинаковы ли значения функции на концах ребер.
Имея полный список раскрасок, можно найти среди них такие, для которых
количество значений функции минимально.
Существует знаменитая теорема Эйлера о раскраске плоских графов:
всякий плоский граф можно раскрасить
пятью цветами. Нельзя не отметить, что реально пока не найдено ни одного
плоского графа, который нельзя было бы раскрасить четырьмя цветами.
Минимальное число цветов, которым
можно раскрасить данный граф 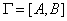 , называется хроматическим
числом данного графа. Обозначается эта характеристика символом , называется хроматическим
числом данного графа. Обозначается эта характеристика символом 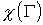 . Найти хроматическое число можно, в частности, перебором
всех раскрасок, о котором говорилось выше. . Найти хроматическое число можно, в частности, перебором
всех раскрасок, о котором говорилось выше.
Можно доказать, что если  обозначает
максимальную локальную степень графа G, то справедливо
неравенство: обозначает
максимальную локальную степень графа G, то справедливо
неравенство: 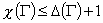 . При этом важно представлять, что равенство . При этом важно представлять, что равенство 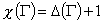 реально возможно для
некоторых G (например, для графа G, представляющего собой две соединенные
вершины), как и неравенство реально возможно для
некоторых G (например, для графа G, представляющего собой две соединенные
вершины), как и неравенство 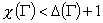 (например для графов
типа «звезды» - (например для графов
типа «звезды» -
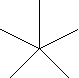
кстати, чем
больше ребер в такой конструкции, тем больше  , а хроматическое число остается равным 2). , а хроматическое число остается равным 2).
Будем обозначать символом 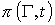 количество раскрасок
графа G с помощью количество раскрасок
графа G с помощью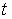 цветов, причем слова
«с помощью цветов, причем слова
«с помощью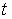 цветов» означают, что
цвета «выбираются» из множества цветов» означают, что
цвета «выбираются» из множества 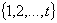 ; ясно, что ; ясно, что 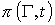 - функция на множестве
натуральных чисел со значениями в том же множестве. Эта функция называется хроматической функцией данного графа. - функция на множестве
натуральных чисел со значениями в том же множестве. Эта функция называется хроматической функцией данного графа.
Нетрудно заметить, что если
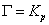 - полный граф на - полный граф на 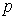 вершинах, то вершинах, то 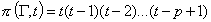 . Таким образом, для полных графов хроматическая функция
является многочленом. Существует теорема Зыкова о хроматических функциях,
благодаря которой возникает практическая возможность построить хроматическую
функцию в явном виде для любого графа. Для формулировки этой теоремы требуется
предварительное разъяснение одного термина. . Таким образом, для полных графов хроматическая функция
является многочленом. Существует теорема Зыкова о хроматических функциях,
благодаря которой возникает практическая возможность построить хроматическую
функцию в явном виде для любого графа. Для формулировки этой теоремы требуется
предварительное разъяснение одного термина.
Фиксируем в графе 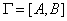 любые две несмежные
вершины любые две несмежные
вершины 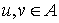 ; слова «стянем (или
склеим) эти вершины в одну вершину» означают построение нового графа ; слова «стянем (или
склеим) эти вершины в одну вершину» означают построение нового графа 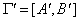 , в котором , в котором 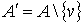 и в котором и в котором 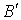 состоит из двух
подмножеств ребер: первое подмножество - это все ребра из состоит из двух
подмножеств ребер: первое подмножество - это все ребра из 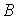 , неинцидентные ни , неинцидентные ни  , ни , ни 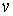 ; второе подмножество состоит из всех ребер, инцидентных ; второе подмножество состоит из всех ребер, инцидентных  , и всех пар , и всех пар 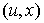 таких, что таких, что 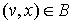 . Геометрически сказанное означает, что вершину . Геометрически сказанное означает, что вершину 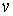 со всеми приходящими в
нее ребрами как бы приклеивают к вершине со всеми приходящими в
нее ребрами как бы приклеивают к вершине  , растягивая при этом некоторые ребра. Вот несколько примеров
стягивания вершин: , растягивая при этом некоторые ребра. Вот несколько примеров
стягивания вершин:
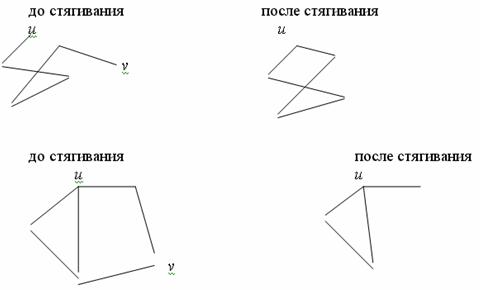
Сформулируем теперь теорему Зыкова:
пусть
в графе 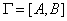 имеются две несмежные вершины имеются две несмежные вершины 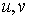 ; тогда хроматическая функция ; тогда хроматическая функция 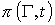 является суммой двух
хроматических функций является суммой двух
хроматических функций  и и 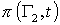 , где граф , где граф 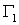 получается из получается из 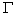 соединением несмежных
вершин соединением несмежных
вершин 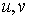 ребром, а граф ребром, а граф 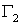 получается из получается из 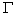 стягиванием вершин стягиванием вершин 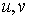 . .
Эта теорема позволяет конструктивно
описывать хроматическую функцию любого графа. При этом следует учитывать, что
хроматическая функция полного графа - это совершенно конкретный объект -
многочлен, - указанный выше. Приступим к построению хроматической функции в
общей ситуации.
Будем хроматическую функцию 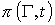 графа G обозначать графической интерпретацией
графа G, т.е. картинкой, изображающей вершины и
соединяющие их ребра. графа G обозначать графической интерпретацией
графа G, т.е. картинкой, изображающей вершины и
соединяющие их ребра.
Таким образом, если, к примеру, граф
G имеет вид
то эта картинка
и будет обозначением функции 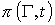 ; если нужно будет записать естественное обозначение 4 ; если нужно будет записать естественное обозначение 4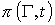 , то будем употреблять символ: , то будем употреблять символ:

Итак, пусть 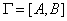 - произвольный граф;
если он полный, то хроматическая функция - произвольный граф;
если он полный, то хроматическая функция 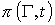 известна; если граф известна; если граф 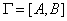 - неполный, то
фиксируем в нем любые две несмежные вершины - неполный, то
фиксируем в нем любые две несмежные вершины 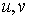 и представим и представим 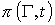 в соответствии с
теоремой Зыкова: в соответствии с
теоремой Зыкова:
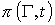 = =  + +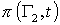 . .
К каждому из слагаемых
в правой части этого равенства повторно применим теорему Зыкова и так далее.
Нетрудно заметить, что эти повторные применения теоремы Зыкова станут
невозможными, когда в правой части окажутся хроматические функции только полных
графов. Поскольку последние описаны явно, постольку и исходная хроматическая
функция получится в явном виде.
Более того, из сказанного следует,
что всякая хроматическая функция является
многочленом (как сумма многочленов). Именно поэтому хроматическую функцию
графа называют его хроматическим
многочленом.
Продемонстрируем пример построения
хроматического многочлена:
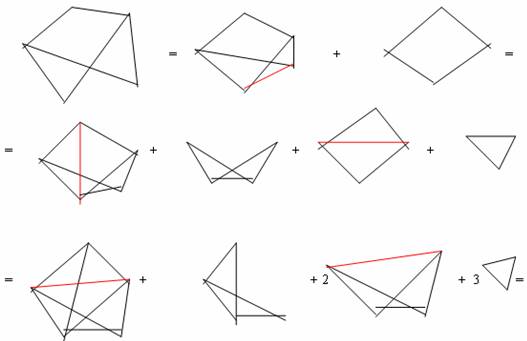
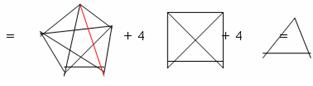
=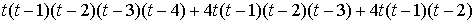 . .
|