|
6. Переход к полярным координатам в двойном интеграле. Полярная система координат
состоит из луча Or . Любая
точка M ? O однозначно определяется
полярным углом ? (0 ? ? <2? или –? < ? £ ?) и полярным
радиусом r (r?0) (рис. 4а).
Для начала координат O радиус r = 0, а
полярный угол не определен.
Пусть декартова полуось Ox совпадает
с полярным лучом Or (рис.4а).
Декартовы координаты выражаются через полярные по
формулам
 (9) (9)
Полярные координаты выражаются через декартовы:
|
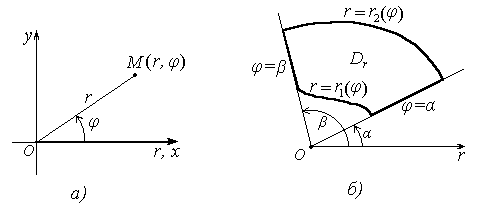
Рисунок 4
|
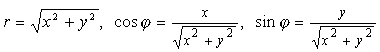 .
(10) .
(10)
Пусть область D
в декартовых координатах преобразуется в область Dr в полярных координатах согласно формулам (10). Тогда
интеграл (1) преобразуется в двойной интеграл в полярных координатах по формуле
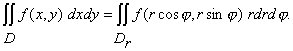 (11)
(11)
Двойной интеграл (11)
вычисляется переходом к повторному интегралу в полярных координатах. Пусть
область Dr имеет вид (рис.
4б)
Dr = { (r, ? ) : ? ? ? ? ?, r1(?) ? r? r2 (?)},
где лучи ? = ? и ? = ? ограничивают сектор, в котором находится фигура Dr , кривые r = r1(?), r =
r2 (?) ограничивают ее в этом секторе. Тогда
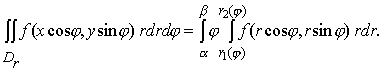 (12) (12)
Замечание. При расстановке пределов
интегрирования в повторном интеграле нужно учесть, что изменение полярного угла
определяется поворотом луча, исходящего из начала O вокруг него против хода
часовой стрелки, а изменение полярного радиуса определяется движением точки
вдоль луча в сторону его возрастания.
|
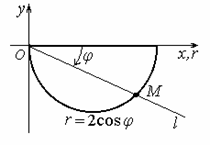
Рисунок 5
|
Примеры. 3). Расставить пределы
интегрирования в повторном интеграле в полярных координатах
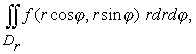
где
Dr - полукруг из рисунка 5.
Решение. Все точки этого полукруга
будут охвачены, если луч Оl будет поворачиваться
от 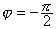 до ? = 0 против хода часовой стрелки.
Значит, до ? = 0 против хода часовой стрелки.
Значит, 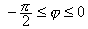 . Пусть теперь луч Оl имеет полярный угол . Пусть теперь луч Оl имеет полярный угол 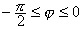 . Тогда при движении точки полукруга по лучу Оl (рис.
5) от точки О до точки M полярный
радиус r изменяется от 0 до координаты r=2cos? точки M. Значит, . Тогда при движении точки полукруга по лучу Оl (рис.
5) от точки О до точки M полярный
радиус r изменяется от 0 до координаты r=2cos? точки M. Значит,
0 ? r ?
2cos ?. Таким образом, Dr = {(r, ?): 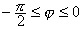 , 0 ? r ? 2 cos ?} . Следовательно, , 0 ? r ? 2 cos ?} . Следовательно,
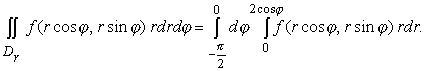
4) Вычислить 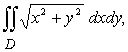 где D = {(x, y): x2 + y2-2x ? 0, y? 0} . где D = {(x, y): x2 + y2-2x ? 0, y? 0} .
Решение.
Подставим в уравнение окружности x2 +y2-2x =
0 полярные
координаты (9) и преобразуем: r2-2 rcos? = 0 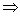 r =2cos?.
Мы получили уравнение полуокружности в полярных координатах из рисунка 5.
Поскольку y? 0, то D - полукруг из примера 3.
Расставим пределы интегрирования как в этом примере и вычислим: r =2cos?.
Мы получили уравнение полуокружности в полярных координатах из рисунка 5.
Поскольку y? 0, то D - полукруг из примера 3.
Расставим пределы интегрирования как в этом примере и вычислим:
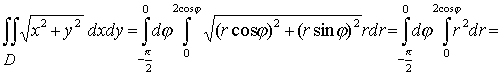
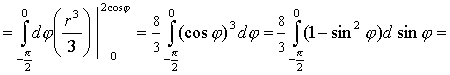
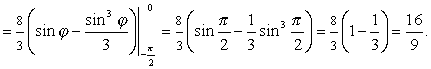
7.
Вычисление площади фигуры. Площадь плоской квадрируемой фигуры D вычисляется по формуле (3)
из пункта 4.
|
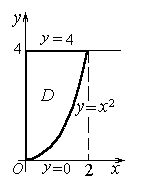
Рисунок 6
|
Пример. 5) Вычислить площадь фигуры,
ограниченной кривыми 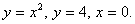
Решение. Данная фигура D расположена в вертикальной полосе
0 ? x ? 2, а в ней ограничена снизу параболой y = x2, сверху - прямой y = 4 (рис. 6). По формуле (5) имеем
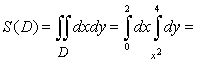 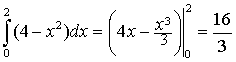 . .
8. Вычисление
объема цилиндрического тела. Если f (x,y)
? 0 в
ограниченной области D, то объем цилиндрического тела (рис.1) вычисляется по
формуле (2) пункта 3.
Пример. 6) Найти объем тела, ограниченного
поверхностями
z = 0,
x2 + y2 = 4, z
= x2 + y2 .
Решение. x2 + y2
= 4 - это круговой цилиндр радиуса 2, ось которого
совпадает с Оy. z = x2 + y2 - параболоид,
который пересекает цилиндр по окружности радиуса 2 в плоскости z = 4 (рис. 7а). z=0 - координатная
плоскость xOy. Таким образом, тело
ограничено сверху параболоидом z = x2 + y2 , снизу - кругом D , с
боков - цилиндрической поверхностью x2 + y2 = 4. Так как данное тело
цилиндрическое и z = x2 + y2 ? 0, то для вычисления его объема можно использовать формулу (2)
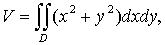
где
D ={ (x, y) : x2 + y2 ? 4, z = 0 }
- круг в плоскости xOy (рис 7б). Для вычисления этого интеграла
перейдем к полярным координатам. При этом круг D преобразуется во множество Dr ={ (r, ?) : 0 ? ? < 2? , 0 ? r ? 2 }. По формуле (12) получим
|
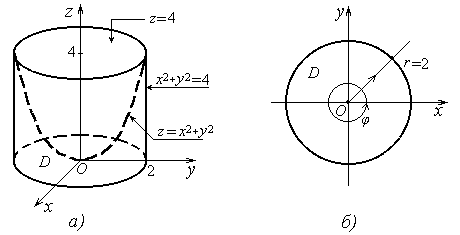
Рисунок 7
|
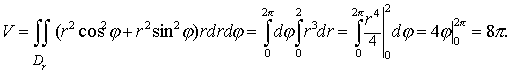
|