|
12.
Переход к цилиндрическим координатам в тройном интеграле.
Пусть в координатной плоскости xOy введена
полярная система координат так, что луч Оr совпадает с полуосью Оx.
Цилиндрическими координатами точки М называются
три числа r, ?, z, где r, ? – полярные
координаты проекции Мz точки М на плоскость xOy, z – аппликата
точки М (рис.
10). Для точек оси Оz координата ? не определена. Декартовы координаты x, y, z выражаются через цилиндрические координаты по формулам
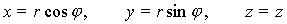 . .
Пусть при переходе к
цилиндрическим координатам тело ?
преобразуется в тело ?ц .
Тогда имеет место формула
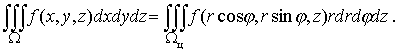 (16)
(16)
|
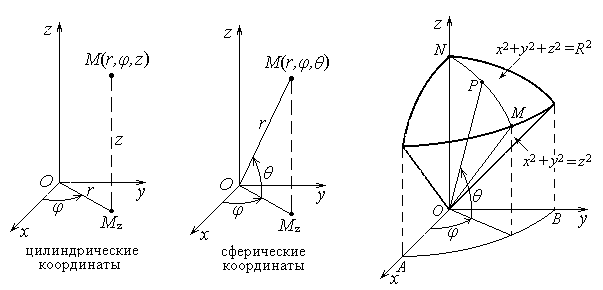
Рисунок 10 Рисунок 11
Рисунок 12
|
Переход к
повторному интегралу в цилиндрических координатах.
Рассмотрим z-цилиндрическое тело ? из рисунка 8. Пусть при переходе к
цилиндрическим координатам множества ?
и D преобразуются
соответственно в ?ц и Dц. Тогда
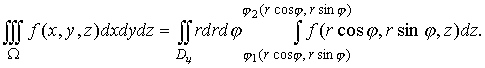 (17) (17)
Пример. 9) Вычислить интеграл
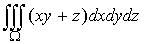
по телу
?, ограниченному поверхностями z = 0, x2 + y2 =
4, z
= x2 + y2 .
Решение. Тело ? изображено на рис. 7. По формуле (16) имеем
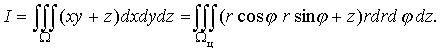
Перейдем
к повторному интегралу по формуле (17). Областью Dц является круг
{(r,?): r
? 2, 0???2?}.
Так как ?1(x, y) ? 0, то ?1(rcos?, rsin?)
? 0. Так как ?2(x, y) ? x2 + y2,
то ?2(rcos?, rsin?)=
(rcos?)2 +(rsin?)2=r2. Следовательно, по формуле (17) получим
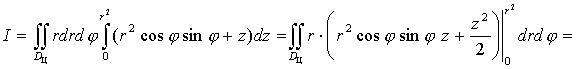
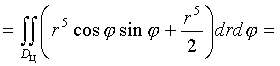 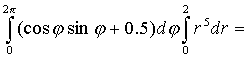
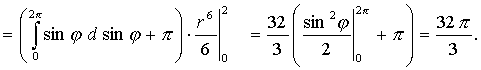
13. Переход к
сферическим координатам в тройном интеграле.
Сферическими
координатами
точки М называются три числа r, ?, ?,
где
r = ОМ (r ?
0) - расстояние от начала координат до точки М,
?
(0 ? ? <
2?) – угол
поворота полуоси Ох вокруг О до совпадения ее направления
с направлением вектора ОМz,
? 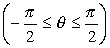 – угол поворота вектора ОМz вокруг О до совпадения его направления с направлением вектора ОМ (рис. 11). – угол поворота вектора ОМz вокруг О до совпадения его направления с направлением вектора ОМ (рис. 11).
Декартовы
координаты связаны со сферическими координатами формулами
x = rcos?
cos?, y =
rsin? cos?, z =
rsin?
Заметим, что ОМ2
= x2+y2+z2 , поэтому в сферических координатах x2+y2+z2 = r2 .
Пусть при переходе к
сферическим координатам тело ?
преобразуется в ?с. Тогда тройной интеграл (13)
преобразуется по формуле
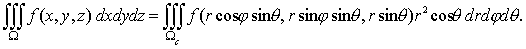 (18) (18)
Второй
интеграл в этой формуле вычисляется переходом к повторному интегралу. Пусть ?с={( r, ?, ?): ?1
? ? ? ?2, ?1(?) ? ? ? ?2(?), r1(?,?) ? r ? r2(?,?)}. Тогда
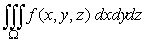 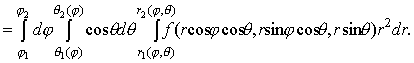 (19) (19)
Пример. 10)
Вычислить объем тела ?, ограниченного
поверхностью
(x2+y2 +z2)2 = a3z
(a > 0).
Решение. Как замечено выше, x2 + y2
+ z2= r2. Поэтому данная поверхность в сферических координатах задается
уравнением r4 = a3rsin?
или 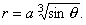 Поскольку a > 0 и r ? 0, то sin? ? 0, т.е. 0 ? ? ? ? /
2. Так как тело ограничено поверхностью Поскольку a > 0 и r ? 0, то sin? ? 0, т.е. 0 ? ? ? ? /
2. Так как тело ограничено поверхностью 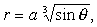 то 0 ? r ? то 0 ? r ? 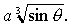 В силу того, что
координата r точки данной поверхности не
зависит от ?, то 0 ? ? ? 2?. Таким образом, ?с={( r, ?, ?):
0 ? ? ? 2?, 0 ? ? ? ?
/ 2, 0 ? r ? В силу того, что
координата r точки данной поверхности не
зависит от ?, то 0 ? ? ? 2?. Таким образом, ?с={( r, ?, ?):
0 ? ? ? 2?, 0 ? ? ? ?
/ 2, 0 ? r ? 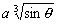 }. }.
Следовательно,
по формулам (14) и (19) получаем
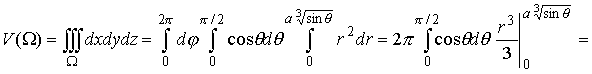
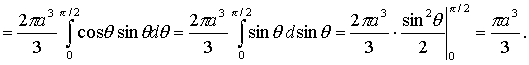
11) Вычислить интеграл
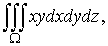 где ? – тело, ограниченное поверхностями x2+y2
+z2=R2, x2+y2 =z2, x=0, y=0 (x?0,
y?0, z?0). где ? – тело, ограниченное поверхностями x2+y2
+z2=R2, x2+y2 =z2, x=0, y=0 (x?0,
y?0, z?0).
Решение.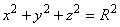 - сфера радиуса R с центром в начале координат. - сфера радиуса R с центром в начале координат. 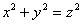 - круговой конус с осью Оу, его образующая наклонена к плоскости
хОу под углом ?/4. Так
как x?0, y?0, z?0, то
тело находится в первом октанте (рис. 12). - круговой конус с осью Оу, его образующая наклонена к плоскости
хОу под углом ?/4. Так
как x?0, y?0, z?0, то
тело находится в первом октанте (рис. 12).
Найдем пределы изменения координат ?,
?, r.
Поскольку проекцией тела ? является сектор ОАВ, то угол ? меняется в пределах 0 ? ? ? ?
? 2.
Пусть теперь угол ? из этого промежутка зафиксирован. Тогда точки тела ? заполняют сектор ОMN , причем отрезок ОM образует с плоскостью хОу угол ? / 4, а ОN – угол ? / 2. Следовательно, угол ? меняется в пределах ? / 4 ? ? ? ? / 2.
При фиксированных значениях углов ? и ? из указанных выше
промежутков точка тела ? пробегает отрезок
ОР от начала координат О до точки
сферы Р. Так как в точке О координата r = 0, а в точке Р r = R , то координата r меняется в пределах 0 ? r ? R .
Таким образом, ?с={( r, ?, ?): 0 ? ? ? ? ? 2, ? ? 4 ? ? ? ? ? 2, 0 ? r ?
R }. Следовательно, по формуле (19) получаем
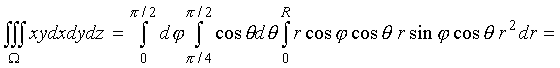
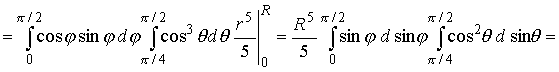
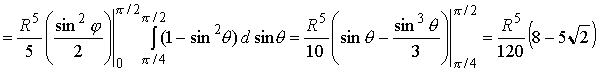 . .
|