Двойные интегралы
1. Записать двойной интеграл от функции f (x,y) по области D, ограниченной прямой y=x и
параболой y=x2, в виде повторных интегралов двумя
способами (по формулам (5) и (7)).
|
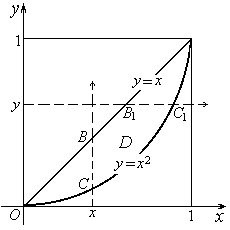
Рисунок 17
|
Решение.
На рисунке 17 изображена область интегрирования D. Для вычисления двойного интеграла по этой области можно воспользоваться
как формулой (5), так и формулой (7), т.к. граница области D пересекается не более, чем в
двух точках как прямыми, параллельными оси Ох,
так и прямыми, параллельными оси Оу.
Применим формулу (5), т.е. внутренний интеграл берем
по y, считая x постоянным, а внешний интеграл – по x. Область D находится в
полосе между прямыми x = 0 и x = 1, следовательно, 0 £ x £ 1. Чтобы найти пределы изменения для y, поступим так: возьмём на оси Ох произвольную точку xÎ(0,1) и проведём через неё
прямую, параллельную оси Оу в направлении
этой оси. Она пересекает границу области D
сначала в точке С, затем в точке В (рис. 17). У точки С ордината y = x2, у точки В ордината y = x , т.е. x2
£ y £ x. Таким образом,
D = {(x, y): 0 £ x £ 1, x2 £ y £ x}. Тогда, согласно (5), имеем:
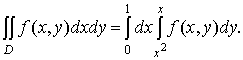
Применим к этому двойному интегралу формулу (7). В
этом случае внутренний интеграл берём по переменной x, считая y постоянным,
а внешний – по y Область D находится в полосе между прямыми y = 0 и y = 1, следовательно, 0 £ y £ 1. Для того, чтобы установить пределы
изменения переменной x, возьмём на
оси Оу произвольную точку yÎ(0,1) и проведём через неё
прямую, параллельную оси Ох в
направлении этой оси. Т.к. точка B1 входа этой прямой в область D имеет абсциссу x
= y, а точка C1 выхода этой прямой из
области D имеет абсциссу 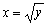 , то переменная x меняется
от y до , то переменная x меняется
от y до 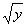 . Значит . Значит
D = {(x, y): 0£ y£1, y £ x £ 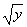 }. Следовательно, согласно (7),
имеем }. Следовательно, согласно (7),
имеем
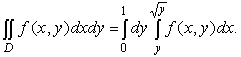
2. Изменить порядок интегрирования в
повторном интеграле
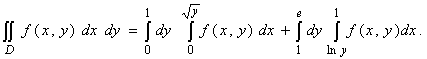
Решение. В отличие от задачи
1), здесь не дана область интегрирования D,
и мы должны выяснить её вид по пределам интегрирования повторных интегралов.
Обозначим D1 - область интегрирования первого повторного
интеграла, D2 - область интегрирования второго повторного
интеграла. Т.к. внутренние интегралы берутся по x, то их пределы показывают, какими линиями области D1 и D2 ограничены справа и слева. Область D1 задаётся неравенствами 0 ? y ? 1, 0 ? x? 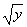 , т.е. D1 = {(x,
y): 0 ? y ? 1, 0 ? x? , т.е. D1 = {(x,
y): 0 ? y ? 1, 0 ? x? 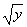 }. Соответственно, область D2 задаётся неравенствами 1 ? y ?
e, lny ? x? 1, т.е. D2 = {(x, y): 1 ? y ? e, lny ? x? 1}. Очевидно, D = D1 È D2
(рис.18). Область D расположена в
вертикальной полосе между прямыми x = 0, x = 1 и
между линиями y = x2, y = ех. Это
значит, что D = {(x, y):
0 ?
x ? 1, x2 ? y? ех}. Тогда по формуле (5) получаем }. Соответственно, область D2 задаётся неравенствами 1 ? y ?
e, lny ? x? 1, т.е. D2 = {(x, y): 1 ? y ? e, lny ? x? 1}. Очевидно, D = D1 È D2
(рис.18). Область D расположена в
вертикальной полосе между прямыми x = 0, x = 1 и
между линиями y = x2, y = ех. Это
значит, что D = {(x, y):
0 ?
x ? 1, x2 ? y? ех}. Тогда по формуле (5) получаем
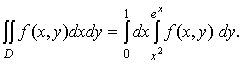
|
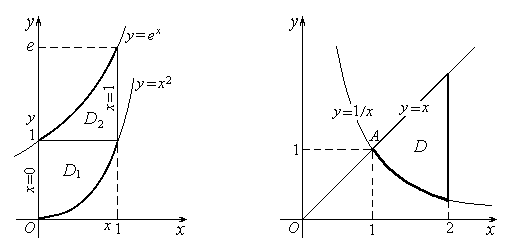
Рисунок 18 Рисунок 19
|
3. Вычислить I = 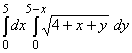 . .
Решение.
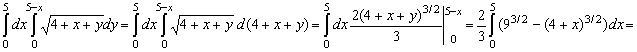
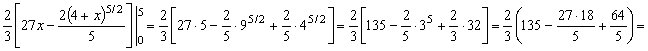
=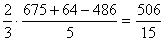 . .
4. Вычислить I
=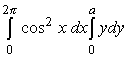 . .
Решение.
I =
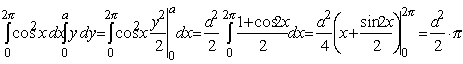 . .
5. Вычислить: I=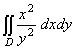 , где D ограничена
прямыми y=x и x=2 и гиперболой xy=1. , где D ограничена
прямыми y=x и x=2 и гиперболой xy=1.
Решение. Область интегрирования
изображена на рисунке 19. Решая систему, состоящую из уравнений прямой y=x и гиперболы xy=1, получим координаты
точки их пересечения А(1,1). Для вычисления интеграла по
области D удобно воспользоваться
формулой (5). Пределы внешнего интеграла по
x – это абсциссы самой левой и самой правой точек области D , т.е. 1 и 2. При 1 £ x £ 2, y
будет изменяться от 1/x до x. Следовательно,
D = { (х; y): 1 £ x £ 2, 1/x £ y £ x }. Тогда
|
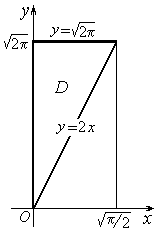
Рисунок 20
|
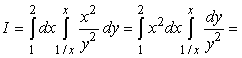
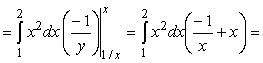
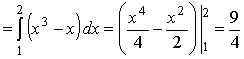 . .
Если применить формулу (7), то
вычисления будут более громоздкими.
6. Вычислить I =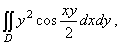 где D - область, ограниченная линиями x=0, y
= где D - область, ограниченная линиями x=0, y
=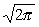 , y =2x. , y =2x.
Решение. Найдём абсциссу точки
пересечения прямых y=2x и
y=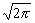 : : 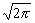 =2x Þ x = =2x Þ x =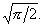 Область
интегрирования D изображена на
рисунке 20. Область
интегрирования D изображена на
рисунке 20.
D =
{(х; y): 0 £ y £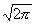 , 0 £ x £ y
/2} , 0 £ x £ y
/2}
По
формуле (7) имеем
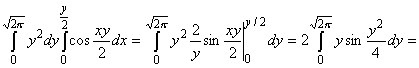
=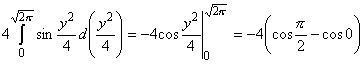 = 4. = 4.
7. Вычислить: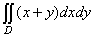 , где D - область,
ограниченная линиями x=0, y=0,
x+y =3. , где D - область,
ограниченная линиями x=0, y=0,
x+y =3.
Решение. Предлагаем студенту
самостоятельно построить область интегрирования. Она имеет вид D = {(х; y): 0 £ x £ 3 , 0£ y £ 3 - x
}. Следовательно, по формуле (5) получаем
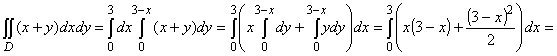
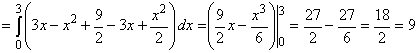 . .
В некоторых случаях, когда область интегрирования D есть круг, или часть круга, или когда
подынтегральная функция содержит в себе двучлен вида x2+y2,
вычисление двойного интеграла упрощается
при переходе к полярным координатам
(см. формулы (9) - (12)). При этом двучлен x2+y2 преобразуется в
r2.
8. Вычислить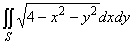 , где S={(x,y): x2+y2£4, y³0}. , где S={(x,y): x2+y2£4, y³0}.
Решение.
Представим уравнение окружности x2+y2=4 в полярных координатах.
По формулам (9) имеем: x2+y2 = 4 Û r 2cos2j +r 2sin
2j = 4 Û r2 = 4
Þ r = 2.
|
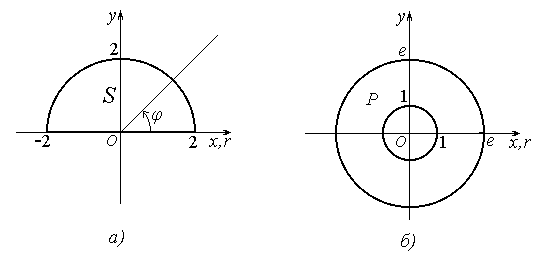
Рисунок 21
|
Расставим пределы интегрирования в повторном
интеграле. Областью интегрирования является
полукруг (рисунок 21,а). Все
точки этого полукруга будут охвачены, если угол j поворачивать от j = 0 до j = p. Значит, при любом 0 £ j £ p, полярный радиус r будет изменяться от 0 до 2.Таким
образом, S = {(r, j): 0 £ j £ p, 0 £ r £ 2}. Cледоватеньно, по формулам (11) и (12)
получим
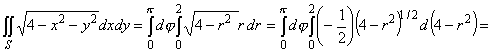
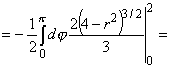 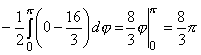 . .
9. Вычислить
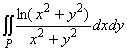 , где P - кольцо между окружностями радиусов е и 1 с центром в начале координат. , где P - кольцо между окружностями радиусов е и 1 с центром в начале координат.
Решение. На рисунке 21,б изображена область P. x2+y2=1, x2+y2=e2 – уравнения заданных окружностей в декартовых
координатах, а в полярной системе эти окружности задаются формулами r =
1 и r = е. Следовательно, Р={(r,j): 0 £ j £ 2p, 1 £ r £ е}. Тогда по формулам (11) и (12) получим
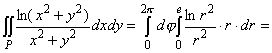
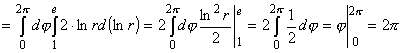 . .
11. Вычислить площадь фигуры, ограниченной линиями y2
= 4 x + 4 , y =
2 – x.
Решение. Данная фигура изображена на рисунке 22,а.
Решая систему уравнений
|
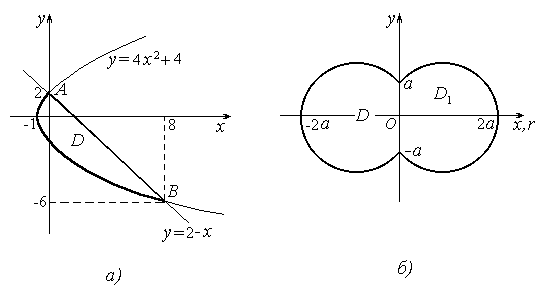
Рисунок 22
|
y2 = 4 x + 4, y = 2 – x, найдём точки пересечения линий: (2 - x) 2= 4x + 4 Û 4 - 4 x+ x2
= 4x+4
Û x2-8 x =
0, x1=0, x2=8, у1=2, у2=-6. Т.о., линии пересекаются в точках A(0,2), B(8,6). Тогда D = {(х, у): - 6 £ у £ 2, (у2 - 4)/4 £ х £ 2 - у}. По формуле (7) имеем
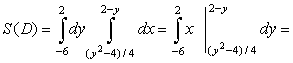
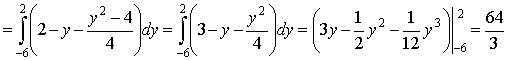 . .
11. Вычислить площадь фигуры, ограниченной линией (х2+ у2)2=а2(4х2+ у2), а>0.
Решение. Очевидно, что кривая
симметрична относительно оси Ох, оси Оу и начала координат. Перейдём к
полярным координатам по формулам (9):
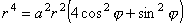 Þ Þ 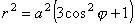 Þ Þ 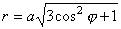 . .
Построим график кривой (рисунок 22,б). В силу симметрии, вся площадь S=4S1, где S1 = S(D1),
D1={(r,j): 0 £ j £ p/2, 0 £ r £ a 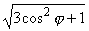 }. Следовательно, }. Следовательно,
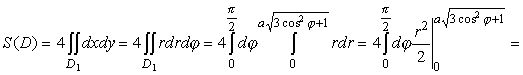
=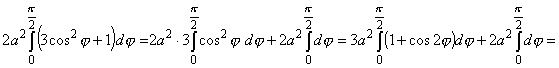
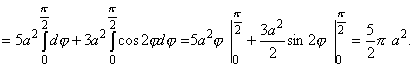
Прежде чем перейти к примерам на
вычисление объёмов, заметим, что при вычислении объёма какого-нибудь тела
полезно сделать пространственный рисунок, который давал бы представление о
форме данного тела. Если же такого рисунка не удаётся построить, то можно
ограничиться хотя бы рисунком, изображающим только область интегрирования на
плоскости xOy. Однако и в этом случае
необходимо представить себе, хотя бы в самых общих чертах, то тело, объём
которого требуется найти.
12. Вычислить объём тела, ограниченного параболоидом
вращения z=x2+y2, координатными
плоскостями и плоскостью x+y =1.
Решение. Поверхность параболоида
вращения z=x2+y2 получается вращением
вокруг оси Oz параболы z=x2. Уравнение x+y =1 в пространстве определяет
плоскость, параллельную оси Oz и
проходящую через прямую x+y =1 в
плоскости хОу. На рисунке 23,а изображено тело, объём которого надо
вычислить. Это тело сверху ограничено
вогнутой поверхностью параболоида z=x2+y2, снизу – плоскостью хОу, спереди - плоскостью x+y =1, слева - плоскостью хОу (y
=0), сзади - плоскостью уОz (x
= 0). Т.к. данное тело цилиндрическое, то для вычисления его объёма можно
использовать формулу (2):
|
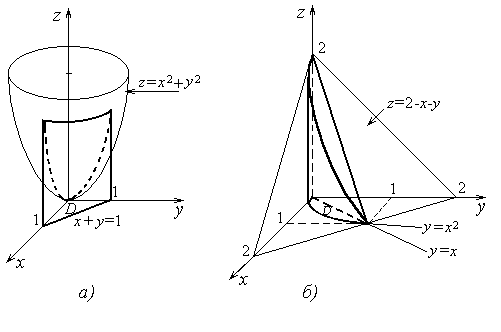
Рисунок 23
|
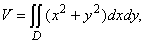
где D = {(x,y): 0£ x£1, 0£ y£1- x} – прямоугольный треугольник. Следовательно,
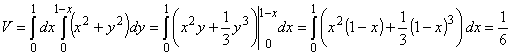 . .
13. Вычислить объём тела, ограниченного поверхностями
z=2–x–y, y=x2, y=x, z=0.
Решение. Поверхность y=x2
– это параболический цилиндр с образующей, параллельной оси Oz, и направляющей параболой y=x2 в плоскости
xOy. Наклонная плоскость z = 2 – x – y отсекает на осях координат равные
отрезки (по две единицы длины). Плоскость y
=x проходит через ось Oz и прямую
y =x в плоскости xOy. z = 0 – уравнение плоскости
xOy. Тело, ограниченное этими
поверхностями, изображено на рисунке 23,б. Т.к. данное тело цилиндрическое и z=2 – x – y,
то
для вычисления его объёма можно использовать формулу (2)
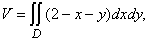
где D = {(x,y): 0£ x£1, x2£ y£ x}. Следовательно,
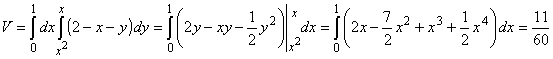 . .
Студенту рекомендуется самостоятельно разобраться,
как получаются пределы интегрирования во внутреннем и внешнем интегралах.
14. Вычислить объём тела, ограниченного
гиперболическим параболоидом z = xy и
плоскостями x + y =а, z=0.
Решение. Заданное тело изображено на
рисунке 24,а. На рисунке 24,б изображена проекция этого тела на
плоскость xOy.
|
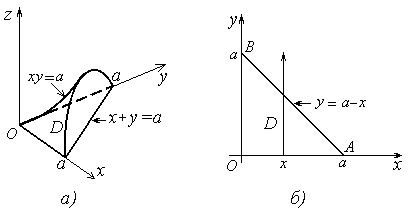
Рисунок 24
|
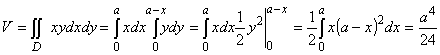 . .
|