|
Тройные интегралы
15. Вычислить I = 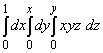 . .
Решение.
I = 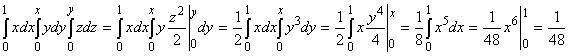 . .
16. Вычислить I
=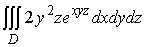 , если D: x =1; y =1; z =1; x = 0; y = 0; z = 0. , если D: x =1; y =1; z =1; x = 0; y = 0; z = 0.
Решение. Областью интегрирования D является единичный куб, три ребра которого лежат на
координатных осях.
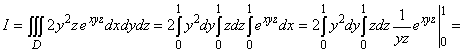
(предлагаем
подумать, почему тройной интеграл удобнее представить в виде повторного именно
в этом порядке)
 . .
|
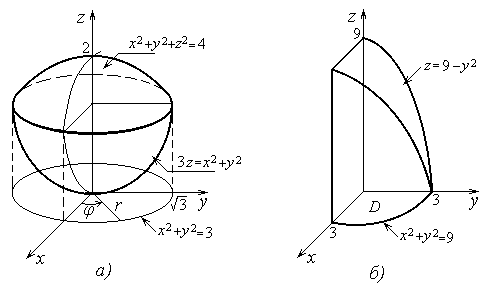
Рисунок 25
|
17. Вычислить объём тела, ограниченного сферой x2+y2+ z2=4 и параболоидом 3z = x2+y2.
Решение.
Пусть W – данное в задаче тело. На
рисунке 25,а изображено тело W1– часть тела W, находящегося в первом
октанте. Очевидно, что V(W) = 4V(W1). Найдём проекцию линии
пересечения сферы и параболоида на плоскость xОy. Для этого достаточно из системы уравнений z2=4-(x2+y2),
z2=(x2+y2)/9
исключить переменную z. В результате
получим 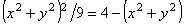 , или , или 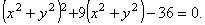 Откуда Откуда 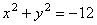 и и 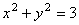 . Следовательно, уравнением проекции будет окружность . Следовательно, уравнением проекции будет окружность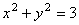 . Согласно формуле
(14) имеем . Согласно формуле
(14) имеем
V(W)=V(W1)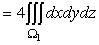
Т.к. проекция данного тела W на плоскость xОy есть круг x2+y2 £ 3, то целесообразно перейти к цилиндрическим
координатам. После преобразований по формулам (16) уравнения окружности x2 + y2 = 3, параболоида 3z = x2+y2 и сферы x2+y2+ z2=4, соответственно, принимают вид 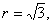 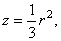 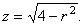 Из рисунка 25,a видно, что в области
интегрирования W1 угол j изменяется от 0 до Из рисунка 25,a видно, что в области
интегрирования W1 угол j изменяется от 0 до 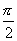 , r - от 0 до , r - от 0 до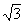 , а z - от , а z - от 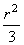 до до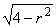 . Поэтому . Поэтому
V(W)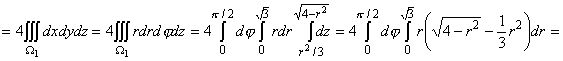
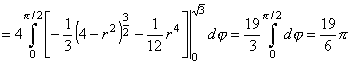 . .
18. Вычислить объём тела, ограниченного поверхностями z = 0, z = 9-y2; x2+y2 =
9.
Решение. Пусть W – данное в задаче тело. На рисунке 25,б изображено тело W1– часть тела W, находящегося в первом
октанте. Очевидно, данное в задаче тело симметрично относительно плоскостей xОz, yОz
и поэтому V(W) = 4V(W1). Согласно формуле (14) имеем V(W)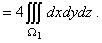 Проекция данной части
тела W1 на плоскость xОy
есть часть круга x2+y2 £ 9, находящегося в первой четверти ( на рис.
25,б – это четверть круга D). Т.о., Проекция данной части
тела W1 на плоскость xОy
есть часть круга x2+y2 £ 9, находящегося в первой четверти ( на рис.
25,б – это четверть круга D). Т.о.,
V(W) = 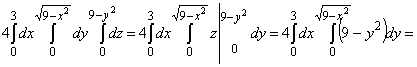 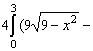
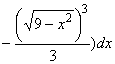 . Сделаем замену x=3sint, dx=3costdt. При x=0, t=0, при x=3, t= . Сделаем замену x=3sint, dx=3costdt. При x=0, t=0, при x=3, t=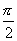 . .
V(W) 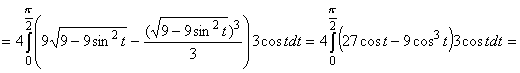
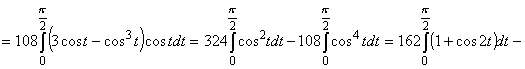
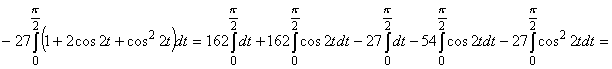
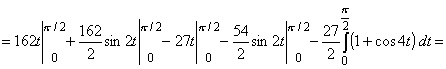
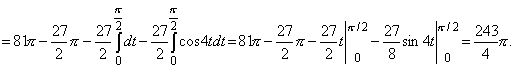
Рекомендуется студенту вычислить
тройной интеграл в цилиндрических координатах и сравнить с вышеприведенным
вычислением по сложности.
Криволинейные
интегралы первого рода
19. Вычислить 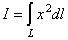 по дуге L плоской кривой y = lnx при 1£ x£ 2. по дуге L плоской кривой y = lnx при 1£ x£ 2.
Решение.
По формуле (23) получим
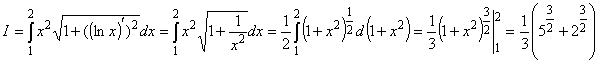 . .
20. Вычислить 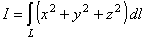 по одному витку винтовой линии L: x = cos t, y =sin t, z = t, 0 £ t £ 2p. по одному витку винтовой линии L: x = cos t, y =sin t, z = t, 0 £ t £ 2p.
Решение. По формуле (23) получим
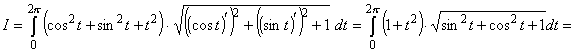
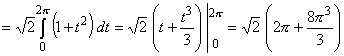 . .
21. Вычислить 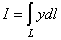 по дуге L параболы y2 = 2x от точки А(0,0) до точки В(2,2). по дуге L параболы y2 = 2x от точки А(0,0) до точки В(2,2).
Решение. Для формулы (22) y = 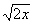 , , 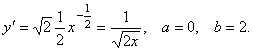
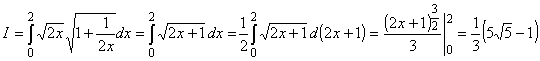 . .
22. Найти массу четверти окружности: x = cos t, y = sin t, расположенной в первом квадранте,
если плотность в каждой точке кривой равна квадрату ординаты этой точки.
Решение. По условию, m(x,y) = y2 =
sin 2 t, dl = 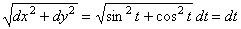
По
формуле (22) имеем
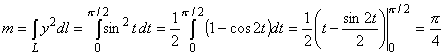 . .
Криволинейные
интегралы второго рода
23. Вычислить 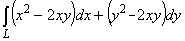 по дуге L параболы y =
x2 от точки А(-1,1) до точки В(2,4). по дуге L параболы y =
x2 от точки А(-1,1) до точки В(2,4).
Решение. Переменная x в данном направлении изменяется от –1
до 2. Вычислим криволинейный интеграл сведением его к определённому:
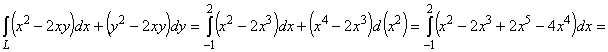
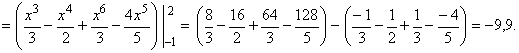
24. Вычислить 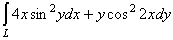 , где L - отрезок прямой, соединяющий точки (0,0) и
(4,8). , где L - отрезок прямой, соединяющий точки (0,0) и
(4,8).
Решение. Найдём уравнение прямой, проходящей через
данные точки:
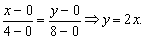
Путь
интегрирования определяется этим уравнением при 0 £ х £ 4. Приняв х за параметр, найдём dy = 2dx и подставим в интеграл значения y и dy.
Получим:
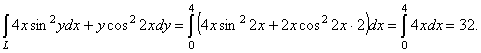
25. Даны точки А
(0,6) и В (3,0). Найти работу,
совершаемую силой 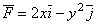 на отрезке АВ. на отрезке АВ.
Решение. Отрезок АВ лежит на прямой: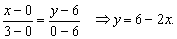 Поскольку Поскольку 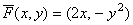 ,то по формуле (27) искомая работа равна ,то по формуле (27) искомая работа равна 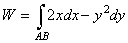 . Приняв в формуле (30)
y =6 - 2x,
dy = - 2dx, a = 0, b = 3, имеем . Приняв в формуле (30)
y =6 - 2x,
dy = - 2dx, a = 0, b = 3, имеем
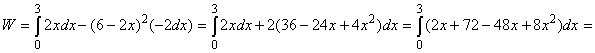
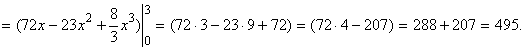
26. Даны точки А(2,0) и В(4,2).
Вычислить I =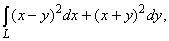 где L - ломаная ОАВ. где L - ломаная ОАВ.
Решение. Интеграл по ломаной равен
сумме интегралов по составляющим её отрезкам. Следовательно,
I =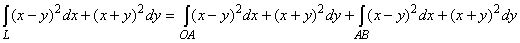 . .
На отрезке ОА
0£х£2, у=0, dy=0, а на АВ 2£х£4, у=х-2, dy=dx.
Поэтому
I
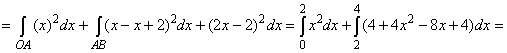
=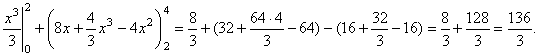
|