11. Функциональные
ряды
11.1 Равномерная
сходимость функционального ряда
Пусть
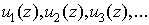 – функции
комплексной переменной z. Ряд – функции
комплексной переменной z. Ряд
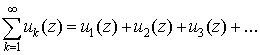
носит название функционального ряда.
Важнейшим понятием для теории таких
рядов является понятие равномерной сходимости.
Пусть
сказано «функциональный ряд сходится в области G». Что это
значит? Это значит, что он сходится в каждой точке этой области, то есть
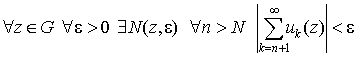 . .
Самым неприятным
является тут то, что 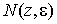 зависит не
только от e,
но и от z. Из-за
этой зависимости ряд может иметь очень неприятные свойства. Желание избавится
от z и приводит к понятию равномерной сходимости функционального
ряда. зависит не
только от e,
но и от z. Из-за
этой зависимости ряд может иметь очень неприятные свойства. Желание избавится
от z и приводит к понятию равномерной сходимости функционального
ряда.
Определение.
Говорят, что функциональный ряд сходится равномерно в области G, если
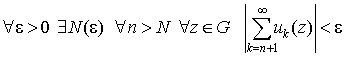 . .
Обратите
внимание на то, куда переместился квантор 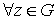 и на то, что
теперь и на то, что
теперь 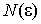 зависит только от e. зависит только от e.
Равномерно сходящиеся ряды обладают
очень хорошими свойствами, которые будут описаны ниже.
Признак
Вейерштрасса. Если существуют такие неотрицательные
числа 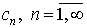 , что , что
1. 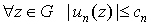 , , 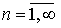 ; ;
2. 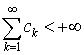 , ,
то ряд 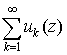 сходится
равномерно в области G. сходится
равномерно в области G.
11.2 Свойства
равномерно сходящихся функциональных рядов
Не давая точных формулировок,
перечислим свойства равномерно сходящихся функциональных рядов.
1. Если все 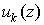 непрерывны в
области G, то сумма ряда непрерывны в
области G, то сумма ряда 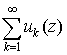 есть также
непрерывная области G функция. есть также
непрерывная области G функция.
2. Если все 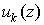 аналитичны в
области G, то сумма ряда аналитичны в
области G, то сумма ряда 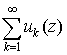 есть также
аналитическая в области G функция. есть также
аналитическая в области G функция.
3. Если ряд 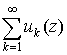 сходится
равномерно в области G, то в нем допустим почленный
переход к пределу, то есть сходится
равномерно в области G, то в нем допустим почленный
переход к пределу, то есть
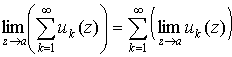 . .
4. Если ряд 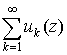 сходится
равномерно в области G, то его можно почленно
интегрировать, то есть сходится
равномерно в области G, то его можно почленно
интегрировать, то есть
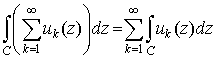 . .
5. Если ряд 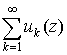 сходится
равномерно в области G, то его можно почленно
дифференцировать любое число раз, то есть сходится
равномерно в области G, то его можно почленно
дифференцировать любое число раз, то есть
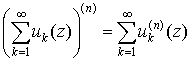 . .
11.3 Степенные ряды
11.3.1 Определение степенного ряда.
Область сходимости
Рассмотрим теперь важнейший частный
случай функционального ряда – так называемый степенной ряд. Он получается,
когда 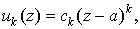 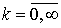 и имеет вид и имеет вид
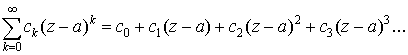 . .
Здесь а и 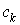 - комплексные числа. - комплексные числа.
Прежде всего, выясним вопрос об области
сходимости степенного ряда.
Теорема.
Для всякого степенного ряда существует такое число 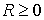 , что степенной ряд сходится при , что степенной ряд сходится при 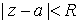 и расходится
при и расходится
при 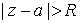 . .
Таким образом, область сходимости
степенного ряда есть круг с центром
в точке а радиуса R, который называется кругом
сходимости (см. рис 11.1). Число R называется радиусом сходимости ряда.
Отметим еще, что общего ответа на
вопрос о сходимости степенного ряда на границе круга сходимости, то есть при 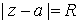 , дать нельзя. В каждом конкретном случае этот вопрос
надо рассматривать отдельно. , дать нельзя. В каждом конкретном случае этот вопрос
надо рассматривать отдельно.
Заметьте еще, что при R=0 степенной ряд сходится только в точке z=a; при R=+¥
степенной ряд сходится на всей плоскости.
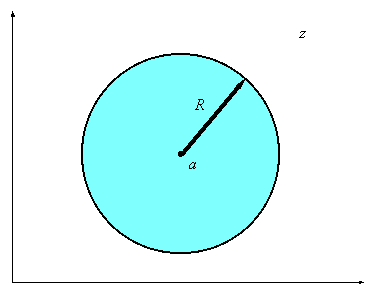
Рис. 11.1 Вид области сходимости
степенного ряда
11.3.2 Нахождение
радиуса сходимости ряда
Важнейшая
характеристика степенного ряда – его радиус сходимости – находится одним из
следующих способов.
1. Если существует 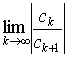 , то , то 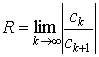 . .
2. Если существует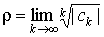 , то , то 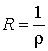 . .
3. Пусть 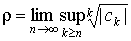 . Тогда . Тогда 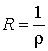 . Эта формула носит название формулы Коши-Адамара и она работает всегда. . Эта формула носит название формулы Коши-Адамара и она работает всегда.
11.3.3 Свойства суммы степенного ряда
Ниже перечислены основные свойства суммы
степенного ряда.
1. Для любого 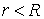 степенной ряд
сходится равномерно в круге степенной ряд
сходится равномерно в круге 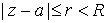 . .
Примечание. r может быть сколь угодно близко к R, но r ¹R !
2. В
круге 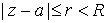 сумма
степенного ряда есть непрерывная функция от z. сумма
степенного ряда есть непрерывная функция от z.
3. При
почленном интегрировании и дифференцировании радиус сходимости степенного ряда
не меняется.
4. В круге 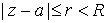 степенной ряд
можно почленно интегрировать любое число раз. степенной ряд
можно почленно интегрировать любое число раз.
5. В круге 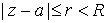 степенной ряд
можно почленно дифференцировать любое число раз. степенной ряд
можно почленно дифференцировать любое число раз.
11.3.4 Разложение
функций в ряд Тейлора
Теорема
1. Пусть  является
аналитической функцией в круге является
аналитической функцией в круге 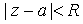 . Тогда внутри этого круга она может быть представлена
в виде ряда . Тогда внутри этого круга она может быть представлена
в виде ряда
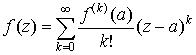 , ,
который сходится
равномерно в любом круге 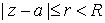 . .
Этот ряд называется рядом Тейлора функции  . .
Теорема
2. Любой степенной ряд является рядом Тейлора своей суммы.
Таким образом, других степенных рядов, кроме
ряда Тейлора, не существует.
11.4 Ряды Лорана
11.4.1 Определение.
Область сходимости
При
разложении функций в ряд Тейлора участвовали только положительные степени
бинома 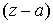 . А почему бы не использовать и отрицательные? . А почему бы не использовать и отрицательные?
Ряды вида
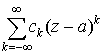
называются
рядами Лорана. Фактически они состоят из двух рядов
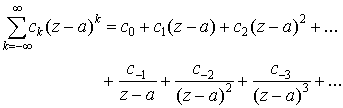 . .
Первый ряд – по
положительным степеням 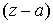 – называется правильной частью ряда Лорана, а второй
ряд – по отрицательным степеням – называется правильной частью ряда Лорана, а второй
ряд – по отрицательным степеням 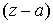 - главной частью ряда Лорана. - главной частью ряда Лорана.
Для сходимости ряда Лорана надо, чтобы
сходилась и его правильная часть, и его главная часть. Это приводит к тому, что
область сходимости ряда Лорана является кольцом
(см. рис. 11.2).
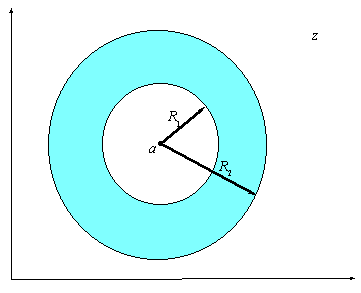
Рис. 11.2 Область сходимости ряда
Лорана
Радиусы
сходимости этого кольца выражаются формулами
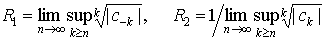 . .
Заметим, что
если 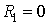 , но в ряде Лорана есть главная часть, то он сходится
в области , но в ряде Лорана есть главная часть, то он сходится
в области 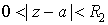 , которая называется «круг с выколотым центром», так
как в точке z = a ряд расходится. , которая называется «круг с выколотым центром», так
как в точке z = a ряд расходится.
11.4.2 Свойства
суммы ряда Лорана
Свойства суммы ряда Лорана аналогичны
свойствам суммы степенного ряда. Они следующие.
1. Пусть 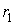 и и 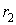 такие, что такие, что 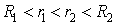 . Тогда в кольце . Тогда в кольце 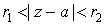 ряд Лорана
сходится равномерно и его сумма является непрерывной функцией. ряд Лорана
сходится равномерно и его сумма является непрерывной функцией.
2. При почленном дифференцировании
и интегрировании ряда Лорана радиусы его кольца сходимости не меняются.
3. В кольце 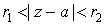 ряд Лорана
можно почленно интегрировать и дифференцировать любое число раз. ряд Лорана
можно почленно интегрировать и дифференцировать любое число раз.
11.4.3 Выражение
для коэффициентов ряда Лорана через его сумму
Обозначим сумму ряда Лорана через  : :
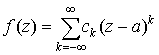 . .
Тогда имеет
место формула
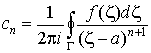 , ,
что и дает явное
выражение для коэффициентов ряда Лорана. Здесь G – любой контур, лежащий
внутри кольца сходимости и охватывающий его «дырку».
|