13. Преобразования Лапласа и
Фурье
13.1 Преобразование
Лапласа – определение и формула обращения
Преобразование
Лапласа является одним из самых мощных
инструментов для решения очень многих прикладных задач в области теории
управления, теории массового обслуживания
и т.д. Часто задача считается решенной, если получено преобразование
Лапласа от искомой функции.
Рассмотрим функцию 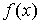 вещественной переменной х. Будем считать, что на эту функцию
наложены следующие ограничения: вещественной переменной х. Будем считать, что на эту функцию
наложены следующие ограничения:
1. 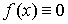 при при 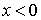 ; ;
2. Существуют такие постоянные М и 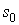 , что , что 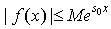 . Константа . Константа 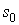 называется показателем роста функции называется показателем роста функции 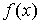 . .
Преобразованием Лапласа от функции 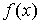 называется
функция называется
функция
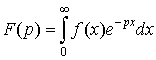
от комплексной переменной 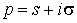 . .
Саму функцию 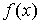 часто называют оригиналом, а функцию часто называют оригиналом, а функцию 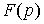 - ее изображением. - ее изображением.
Изображение 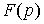 определено в
полуплоскости определено в
полуплоскости 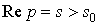 и является в
этой полуплоскости аналитической функцией. и является в
этой полуплоскости аналитической функцией.
Самым принципиальным является то, что
не только 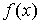 однозначно определяет однозначно определяет
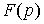 , но и наоборот, , но и наоборот, 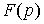 однозначно
определяет однозначно
определяет 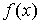 . Это соответствие дается так называемой формулой обращения или формулой Меллина. Она имеет вид . Это соответствие дается так называемой формулой обращения или формулой Меллина. Она имеет вид
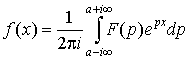 . .
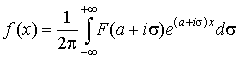 . .
Таким
образом, существует взаимно однозначное соответствие 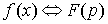 . И хотя формула Меллина не является рабочей формулой –
для вычисления оригинала . И хотя формула Меллина не является рабочей формулой –
для вычисления оригинала 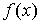 по изображению по изображению 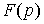 обычно
пользуются специальными таблицами и свойствами преобразования Лапласа – ее
значение именно в гарантии этого взаимно
однозначного соответствия обычно
пользуются специальными таблицами и свойствами преобразования Лапласа – ее
значение именно в гарантии этого взаимно
однозначного соответствия 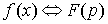 . .
13.2 Свойства
преобразования Лапласа
В
приводимых ниже формулах 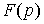 и и 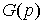 являются
преобразованиями Лапласа от функций являются
преобразованиями Лапласа от функций 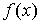 и и 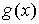 соответственно. соответственно.
1. Линейность.
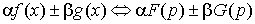 . .
2. Теорема подобия.
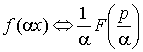 . .
3. Дифференцирование оригинала.
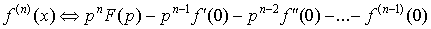 . .
Именно это свойство и обеспечило такую популярность преобразованию
Лапласа: оно операцию дифференцирования оригинала
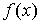 заменяет операцией умножения изображения на p. Это, конечно, сильно упрощает решение задач, где есть
производные. заменяет операцией умножения изображения на p. Это, конечно, сильно упрощает решение задач, где есть
производные.
4. Дифференцирование
изображения.
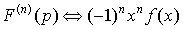 . .
5. Интегрирование оригинала.
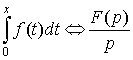 . .
Наряду со свойством 3, это свойство
является основным для приложений преобразования Лапласа, так как оно заменяет
сложную операцию интегрирования оригинала операцией деления изображения на p.
6. Интегрирование изображения.
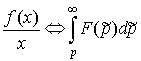 . .
7. Теорема запаздывания.
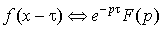 . .
8. Теорема смещения.
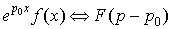 . .
9. Теорема умножения.
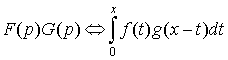 . .
Комбинация 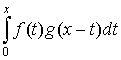 называется сверткой функций называется сверткой функций 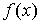 и и 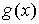 и обозначают
символом и обозначают
символом 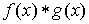 . Эта операция также встречается очень часто при
решении прикладных задач, и преобразование Лапласа позволяет заменить операцию свертки двух оригиналов операцией умножения их изображений. . Эта операция также встречается очень часто при
решении прикладных задач, и преобразование Лапласа позволяет заменить операцию свертки двух оригиналов операцией умножения их изображений.
10. Предельные соотношения.
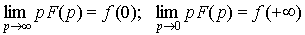 . .
13.3 Преобразование Фурье – определение
и формула обращения
Кроме преобразования Лапласа, широкое
применение находит также еще одно интегральное преобразование, которое носит
название преобразования Фурье.
Пусть 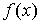 есть функция
вещественной переменной х,
определенная на всей прямой есть функция
вещественной переменной х,
определенная на всей прямой 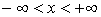 . Основное ограничение, накладываемое на эту функцию,
имеет вид . Основное ограничение, накладываемое на эту функцию,
имеет вид
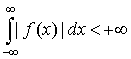 , ,
то есть эта
функция абсолютно интегрируема на всей числовой оси. Кроме этого, требуется,
чтобы 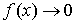 при при 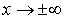 . .
Преобразованием
Фурье 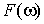 от функции от функции 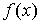 называется
функция называется
функция
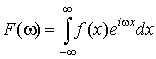 . .
Она существует
при любых w.
Как и в случае преобразования Лапласа
оказывается, что не только 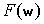 однозначно
определяется функцией однозначно
определяется функцией 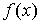 , но и наоборот, , но и наоборот, 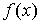 однозначно определяется однозначно определяется
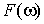 , то есть имеется взаимно однозначное соответствие , то есть имеется взаимно однозначное соответствие 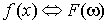 . Это соответствие дается формулой обращения, которая имеет вид . Это соответствие дается формулой обращения, которая имеет вид
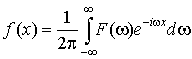 . .
В ней
несобственный интеграл понимается в смысле главного значения. Сама формула
носит название обратного преобразования
Фурье.
13.4 Свойства
преобразования Фурье
Пусть 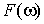 и и 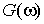 есть
преобразования Фурье от функций есть
преобразования Фурье от функций 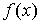 и и 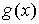 соответственно,
то есть соответственно,
то есть 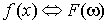 и и 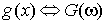 . .
1. Линейность.
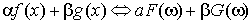 . .
2. Теорема подобия.
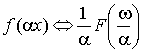
3. Теорема о сдвиге.
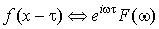 . .
4. Формула смещения.
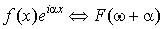 . .
5. Дифференцирование функции.
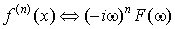 . .
6. Дифференцирование преобразования Фурье.
Если 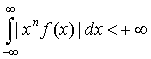 , то , то
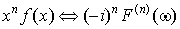 . .
7. Свертка функций.
Пусть
функции 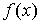 и и 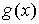 определены для определены для 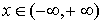 . Сверткой
этих двух функций называется интеграл . Сверткой
этих двух функций называется интеграл
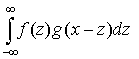 , ,
который
обозначается 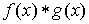 . .
Соответствующее свойство преобразования
Фурье имеет вид
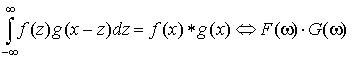 . .
|