5. Определенный интеграл
5.1 Определение
определенного интеграла
Пусть
на отрезке [a, b] задана
функция f(x).
Построение понятия определенного интеграла от этой функции по отрезку [a, b] состоит из трех этапов.
1. Разбиение отрезка [a, b] на части.
Разобьем отрезок [a, b] на части точками 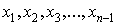 так что так что
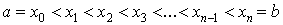
(см. рис. 5.1).

Рис. 5.1 Схема разбиения отрезка [a, b] на части
Обозначим через 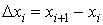 длину i-го кусочка и через длину i-го кусочка и через 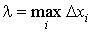 максимальную из
этих длин. максимальную из
этих длин.
2. Построение
интегральной суммы.
Выберем
на каждом отрезке 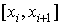 произвольным образом некоторую точку произвольным образом некоторую точку 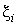 так что так что 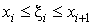 (она называется «средней точкой»), и составим (она называется «средней точкой»), и составим
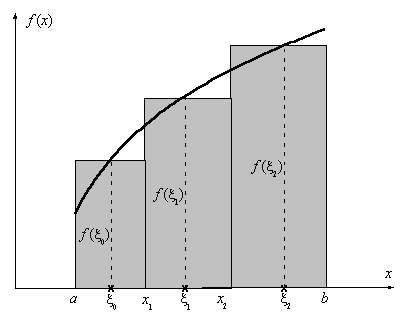
Рис. 5.2 Геометрический смысл
интегральной суммы
величину, которая называется интегральной суммой
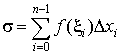 . .
Геометрически она
представляет собой сумму площадей прямоугольников с основаниями в виде отрезков
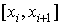 и высотами и высотами 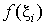 (см. рис. 5.2). (см. рис. 5.2).
3. Предельный переход.
Найдем теперь предел
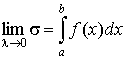 . .
Определение.
Если существует 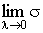 и он не зависит
от и он не зависит
от
а) способа разбиения отрезка 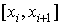 на части и от на части и от
б) способа выбора средней точки,
то говорят, что 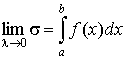 есть определенный интеграл от функции f(x) по отрезку [a, b]. есть определенный интеграл от функции f(x) по отрезку [a, b].
Функция f(x) называется в этом случае интегрируемой на отрезке [a, b].
Величины a и b
называются нижним и верхним пределами интегрирования соответственно.
5.2 Суммы
Дарбу. Классы интегрируемых функций
Пусть 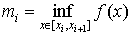 и и 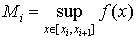 . Составим суммы . Составим суммы
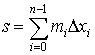 и и 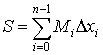 . .
Они называются
суммами Дарбу.
Тогда верна следующая
Теорема.
Для существования определенного интеграла необходимо и достаточно, чтобы 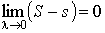 . .
Эта теорема позволяет установить классы
интегрируемых функций.
Теорема
1. Если f(x)
ограничена на [a, b] и имеет
на нем лишь конечное число точек разрыва, то она интегрируема на [a, b].
Теорема 2. Если f(x) монотонна и ограничена на [a, b], то она интегрируема на [a, b].
5.3 Свойства
определенных интегралов
Ниже перечислены основные свойства
определенного интеграла.
1. 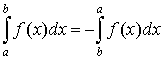 ; ;
2. если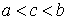 , то , то 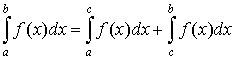 ; ;
3. 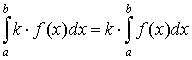 ; ;
4. 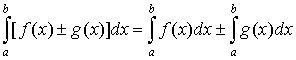 ; ;
5. 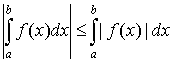 ; ;
6. если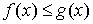 , то , то 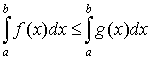 . .
5.5 Первая
теорема о среднем
Теорема.
Пусть
1.
f(x) и g(x) интегрируемы на [a, b];
2.
существуют такие конечные m и M, что 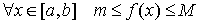 ; ;
3.
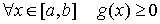 . .
Тогда существует
m
такое, что
1. 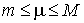 ; ;
2. 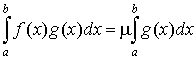 . .
Следствие. Если f(x) непрерывна на [a, b], то
существует такое cÎ[a, b], что
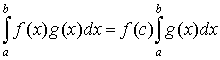 . .
Частный
случай. Пусть g(x) = 1
и f(x) непрерывна на [a, b]. Тогда существует такое cÎ[a, b], что
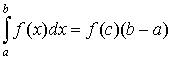 . .
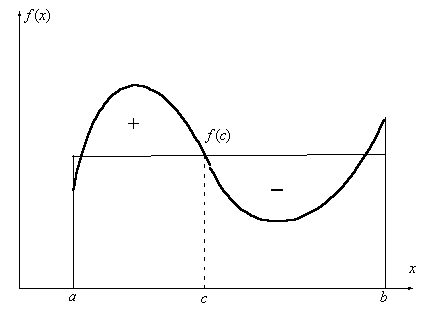
Рис. 5.3 Геометрическая интерпретация
первой теоремы о среднем
Геометрически
это означает, что существует cÎ[a, b], такое, что площадь криволинейной трапеции
ограниченной графиком кривой f(x) и
отрезком [a, b] равна
площади прямоугольника с основанием [a, b] и
высотой, равной f(с).
5.6 Вычисление
определенных интегралов.
Формула
Ньютона-Лейбница.
Если
существует непрерывная F(x) такая, что 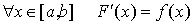 , то , то
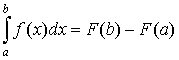 . .
Интегрирование
по частям.
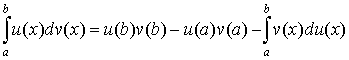 . .
Замена
переменных в определенном интеграле.
Теорема.
Пусть
1.
f(x)
интегрируема на [a, b];
2.
j(t) монотонно возрастает и j(a)=a, j(b)=b;
3.
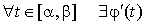 . .
Тогда
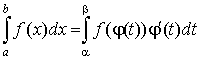 . .
5.7 Определенный интеграл как
функция верхнего предела
Обратите внимание на то, что
1. 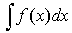 это функция от х, а это функция от х, а 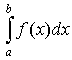 это число. это число.
2. Значение определенного интеграла не зависит от того, какой буквой
обозначена переменная интегрирования, то есть
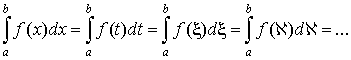 . .
Однако если сделать пределы
интегрирования переменными, мы получим уже функцию этих пределов.
Рассмотрим свойства функции от х
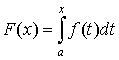 . .
Теорема
1. Пусть f(x) интегрируема на [a, b]. Тогда F(x) есть непрерывная функция на [a, b].
Теорема
2. Если f(x) непрерывна на [a, b], то существует 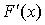 и и 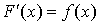 . .
Таким образом, у каждой непрерывной функции существует первообразная.
Аналогичными свойствами обладает и 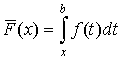 , только для нее , только для нее 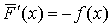 . .
5.8 Геометрические
приложения определенного интеграла
5.8.1 Длина
дуги кривой.
5.8.1.1 Определение
длины дуги.
Пусть на плоскости задана некоторая
кривая АВ. Прежде всего надо описать
ее математически. Самым общим заданием плоской кривой считается ее
параметрическое задание, когда кривая задается системой
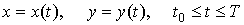 . .
Разобьем отрезок 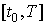 на части на части
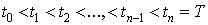 , ,
и пусть 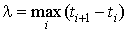 . Тогда вся кривая АВ
разобьется на кусочки точками Мi, . Тогда вся кривая АВ
разобьется на кусочки точками Мi, 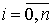 (см. рис. 5.4). (см. рис. 5.4).

Рис. 5.4 К определению длины дуги
плоской кривой
Соединим точки 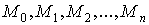 отрезками
прямых, и пусть li есть
длина отрезка прямой, соединяющей точки Mi и Mi+1. Найдем периметр вписанной ломаной отрезками
прямых, и пусть li есть
длина отрезка прямой, соединяющей точки Mi и Mi+1. Найдем периметр вписанной ломаной
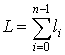 . .
Если существует 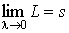 и этот предел
не зависит от способа разбиения отрезка и этот предел
не зависит от способа разбиения отрезка 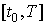 на кусочки, то он называется длиной дуги кривой АВ. на кусочки, то он называется длиной дуги кривой АВ.
5.8.1.2 Вычисление
длины дуги.
Теорема.
Пусть функции x(t) и y(t) имеют на отрезке 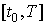 непрерывные производные непрерывные производные 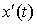 и и 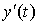 . Тогда длина дуги кривой . Тогда длина дуги кривой
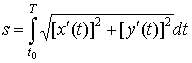 . .
Частные
случаи.
1. Явное задание кривой.
В этом случае кривая задается в виде 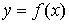 , , 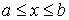 , и длина ее
дуги равна , и длина ее
дуги равна
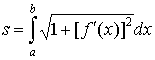 . .
2. Кривая в полярных
координатах. Уравнение кривой имеет в этом случае вид 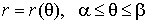 и длина ее дуги
равна и длина ее дуги
равна
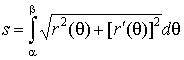 . .
5.8.1.3 Длина
дуги пространственной кривой.
В
трехмерном пространстве кривая задается в виде 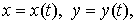 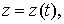 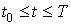 и длина ее дуги
равна и длина ее дуги
равна
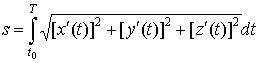 . .
5.8.2 Площади
криволинейных трапеции и сектора
Криволинейной трапецией называется
фигура, изображенная на рис. 5.5.

Рис. 5.5 Криволинейная трапеция
Ее площадь равна
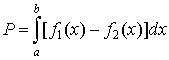 . .
Криволинейным сектором называется
фигура, изображенная на рис. 5.6.
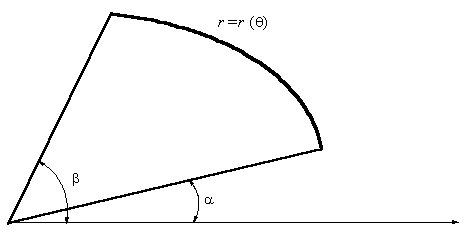
Рис. 5.6 Криволинейный сектор
Его площадь
равна
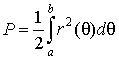 . .
5.8.3 Объем
и поверхность тела вращения.
Пусть
на плоскости дана кривая, заданная параметрически
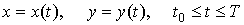 , ,
и это кривая
вращается вокруг оси ОХ. Получающееся
тело носит название тела вращения. Оно напоминает бочку (см. рис. 5.7).
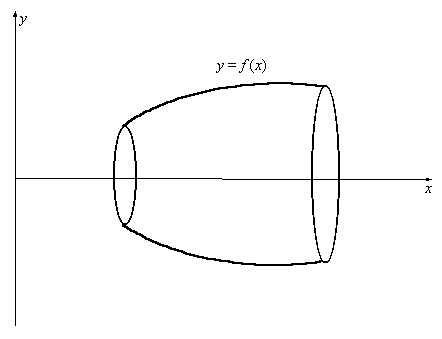
Рис. 5.7 Тело вращения
Его объем равен
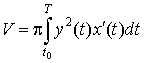 , ,
а боковая
поверхность равна
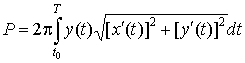 . .
Если кривая
задана явно 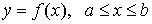 , то соответствующие выражения принимают вид , то соответствующие выражения принимают вид
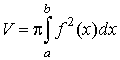 , , 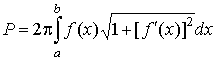 . .
|