7. Числовые ряды
7.1 Определение и простейшие свойства
числовых рядов
Пусть задана бесконечная
последовательность вещественных чисел 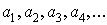 . Построим
последовательность . Построим
последовательность
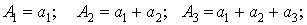 … … 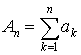
и рассмотрим
предел этой последовательности
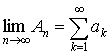 . .
Он называется
числовым рядом, или просто рядом. Если этот предел существует и конечен, то
говорят, что ряд сходится, или, что
ряд существует. Если этот предел
равен бесконечности или вообще не существует, то говорят, что ряд расходится, или, что ряд не существует.
Величины An называются частными
суммами ряда. Слагаемое an называется общим
членом ряда. Ряды 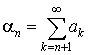 называются остатком ряда после n-го слагаемого. называются остатком ряда после n-го слагаемого.
Простейшие
свойства сходящихся рядов.
1. Если ряд сходится, то сходится любой из его остатков. Наоборот,
из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует,
что изменение или выбрасывание конечного
числа членов ряда не изменяет его сходимости или расходимости.
2. Если ряд 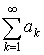 сходится, то сходится, то 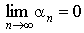 . .
3. Если ряд 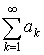 сходится, то
сходится ряд сходится, то
сходится ряд 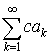 и имеет место
равенство и имеет место
равенство
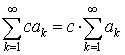 . .
4. Если ряды 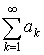 и и 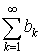 сходятся, то
сходится и ряд сходятся, то
сходится и ряд 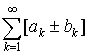 имеет место
равенство имеет место
равенство
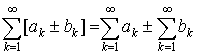 . .
5. Если ряд 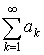 сходится, то сходится, то 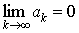 . .
Отсюда следует
Признак расходимости ряда. Если 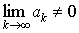 , то ряд , то ряд 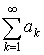 расходится. расходится.
7.2 Теоремы о рядах с положительными
слагаемыми
В данном разделе рассматриваются два
ряда - 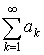 и и 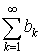 , которые будут
называться «ряд А» и «ряд В» соответственно. Считается что все их
слагаемые положительны, то есть , которые будут
называться «ряд А» и «ряд В» соответственно. Считается что все их
слагаемые положительны, то есть 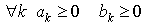 . .
Теорема
1. Если, начиная с некоторого N, имеет место неравенство 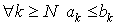 , то из сходимости ряда В следует сходимость ряда А,
а из расходимости ряда А следует
расходимость ряда В. , то из сходимости ряда В следует сходимость ряда А,
а из расходимости ряда А следует
расходимость ряда В.
Теорема
2. Пусть существует
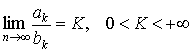 . .
Тогда ряды А и В
либо одновременно сходятся, либо одновременно расходятся.
Теорема
3. Если, начиная с некоторого N, имеет место неравенство
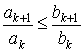 , ,
то из сходимости
ряда В следует сходимость ряда А, а из расходимости ряда А следует расходимость ряда В.
7.3 Признаки
сходимости рядов с положительными членами
Пусть
дан ряд 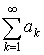 все слагаемые
которого положительны все слагаемые
которого положительны 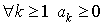 . .
Признак
Коши. Пусть существует 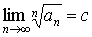 . Тогда . Тогда
если 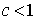 , то ряд , то ряд 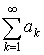 сходится; сходится;
если 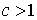 , то ряд , то ряд 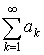 расходится; расходится;
если 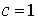 , то о сходимости или расходимости ряда ничего сказать
нельзя. , то о сходимости или расходимости ряда ничего сказать
нельзя.
Признак
Даламбера. Пусть существует 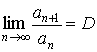 . Тогда . Тогда
если 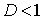 , то ряд , то ряд 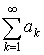 сходится; сходится;
если 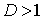 , то ряд , то ряд 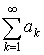 расходится; расходится;
если 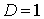 , то о сходимости или расходимости ряда ничего сказать
нельзя. , то о сходимости или расходимости ряда ничего сказать
нельзя.
7.4 Интегральный
признак Коши
Пусть
f(x) – некоторая функция, определенная
на интервале [1, ¥).
В этом разделе рассматриваются ряды вида 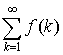 , то есть ряды со слагаемыми вида , то есть ряды со слагаемыми вида 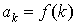 . .
Интегральный
признак Коши. Пусть при x®¥ функция f(x) монотонно убывает до нуля, то есть 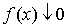 . Тогда ряд . Тогда ряд 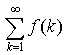 сходится или
расходится одновременно с интегралом сходится или
расходится одновременно с интегралом 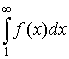 . .
Дополнительные
формулы.
1. Пусть ряд 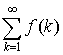 сходится. Тогда для его остатка имеет
место следующая оценка сходится. Тогда для его остатка имеет
место следующая оценка
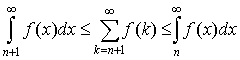 . .
2. Пусть ряд 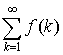 расходится, то есть расходится, то есть 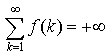 . Тогда для его частных сумм имеет место представление . Тогда для его частных сумм имеет место представление
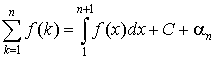 , ,
где C – некоторая константа, а 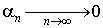 . .
7.5 Знакопеременные
ряды
Пусть
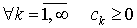 . Рассмотрим ряды вида . Рассмотрим ряды вида
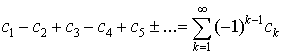 . .
Они называются знакопеременными рядами.
Признак
Лейбница. Если при 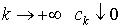 , то ряд , то ряд 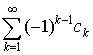 сходится. сходится.
Для этого случая имеет место следующая
оценка остатка ряда
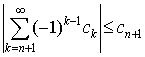 , ,
то есть остаток
ряда меньше первого отброшенного слагаемого.
7.6 Ряды
со слагаемыми произвольного знака
Пусть теперь отдельные слагаемые 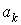 ряда ряда 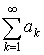 имеют
произвольный знак. имеют
произвольный знак.
Теорема.
Если ряд 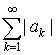 сходится, то
ряд сходится, то
ряд 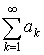 также сходится. также сходится.
Определение.
Если ряд 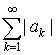 сходится, то
ряд сходится, то
ряд 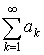 называется абсолютно сходящимся. Если ряд называется абсолютно сходящимся. Если ряд 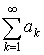 сходится, а сходится, а 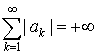 , то ряд , то ряд 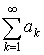 называется неабсолютно сходящимся. называется неабсолютно сходящимся.
Признак
Дирихле. Пусть все частные суммы ряда 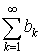 ограничены (то
есть ограничены (то
есть 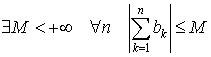 ), а ), а 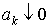 при при 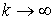 . Тогда ряд . Тогда ряд 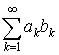 сходится. сходится.
Следствие.
Если 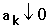 при при
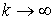 , то сходятся ряды , то сходятся ряды 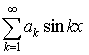 и и 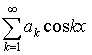 (последний при (последний при 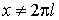 ). ).
7.7 Сочетательное
свойство сходящихся рядов
Пусть дан ряд
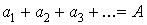 , ,
который мы будем
называть «ряд А» и ряд
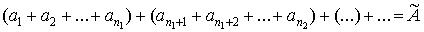 , ,
который мы будем
называть «ряд 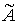 ». Он отличается от ряда А тем, что в нем слагаемые объединены в группы, что проявляется в
том, что они заключены в скобки. ». Он отличается от ряда А тем, что в нем слагаемые объединены в группы, что проявляется в
том, что они заключены в скобки.
Теорема.
Если ряд А сходится, то ряд 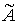 тоже сходится и
имеет ту же сумму. тоже сходится и
имеет ту же сумму.
Однако важно помнить следующее:
1. Обратная операция – раскрытие скобок - вообще говоря, незаконна,
так как из сходящегося ряда может получиться ряд расходящийся. Например, раскрывая
скобки в ряде
(1–1)+(1–1)+(1–1)+…
мы получим
расходящийся ряд
1–1+1–1+1–1±…
Раскрывать
скобки можно лишь тогда, когда доказано, что получающийся после раскрытия
скобок ряд сходится.
2. Это свойство неверно для расходящихся
рядов, то есть при объединении слагаемых в группы может получиться сходящийся
ряд, и его сумма может быть разной. Например, в расходящемся ряде
1–1+1–1+1–1±…
можно объединить
слагаемые в группы так
(1–1)+(1–1)+(1–1)+…=0
и получающийся
ряд будет иметь сумму 0. Если же объединить слагаемые в группы так
1–(1–1)–(1–1)–(1–1)–…
=1
то получающийся
ряд будет иметь сумму 1.
7.8 Переместительное
свойство сходящихся рядов
Рассмотрим
ряд
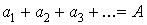 , ,
который мы будем
называть «ряд А».
Пусть 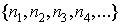 есть некоторая
перестановка из чисел есть некоторая
перестановка из чисел 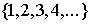 , в которой переставлено бесконечно много чисел. Рассмотрим ряд , в которой переставлено бесконечно много чисел. Рассмотрим ряд
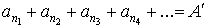 , ,
который мы будем
называть «ряд 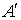 ». ».
Теорема.
Если ряд А абсолютно сходится, то ряд 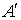 также абсолютно
сходится и имеет ту же сумму. также абсолютно
сходится и имеет ту же сумму.
Теорема
Римана. Если ряд А сходится неабсолютно, то, какое бы ни взять
число В (конечное, или равное ±¥)
можно так переставить слагаемые в ряде А,
что его сумма станет равна В.
Таким образом, в неабсолютно сходящемся
ряде перестановка бесконечного числа
слагаемых недопустима.
|