9. Криволинейные и кратные
интегралы
9.1 Криволинейные интегралы первого рода
9.1.1 Определение
криволинейного интеграла первого рода
Пусть
на плоскости XOY заданы
1. Некоторая кривая С с граничными точками А и В;
2. Функция двух переменных f(x, y),
определенная, по крайней мере, на кривой С.
Проделаем следующую процедуру, которая
является стандартной для построения определенного интеграла (см. рис. 9.1).
1. Разобьем кривую С на кусочки точками 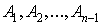 и точку А будем считать точкой и точку А будем считать точкой 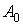 , а точку В
– точкой , а точку В
– точкой 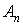 . .

Рис. 9.1 К построению понятия
криволинейного интеграла первого рода
Пусть 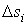 есть длина дуги
кривой С между точками есть длина дуги
кривой С между точками 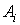 и и 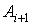 и и 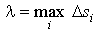 . .
2. На каждом отрезке кривой С между точками 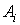 и и
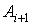 выберем произвольным
образом «среднюю точку» с координатами выберем произвольным
образом «среднюю точку» с координатами 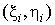 и составим интегральную
сумму и составим интегральную
сумму
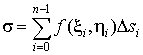 . .
3. Сделаем предельный переход при 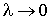 . Если существует . Если существует 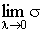 и он не зависит
от способа разбиения кривой С на
кусочки и от способа выбора средней точки, то он называется криволинейным
интегралом первого рода от функции f(x, y) по кривой С и
обозначается символом и он не зависит
от способа разбиения кривой С на
кусочки и от способа выбора средней точки, то он называется криволинейным
интегралом первого рода от функции f(x, y) по кривой С и
обозначается символом
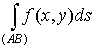 . .
Заметьте, что
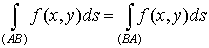 . .
9.1.2 Вычисление криволинейного интеграла первого
рода
Пусть кривая АВ задана параметрически в виде
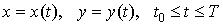 . .
Тогда формула
для вычисления криволинейного интеграла первого рода имеет вид
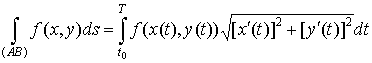 . .
Если кривая
задана явно в виде 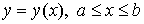 , то , то
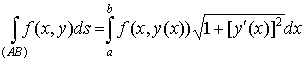 . .
Если кривая
задана в полярных координатах 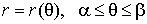 , то , то
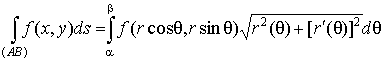 . .
9.1.3 Пространственные
кривые
Криволинейный
интеграл первого рода по пространственной кривой определяется совершенно аналогично
криволинейному интегралу по плоской кривой. Если пространственная кривая задана
параметрически
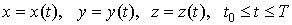 , ,
то
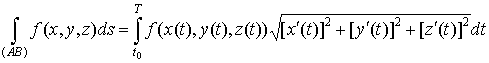 . .
9.2 Криволинейные
интегралы второго рода
9.2.1 Определение
криволинейного интеграла второго рода
Пусть
снова на плоскости XOY задана кривая АВ, которая проходится в направлении от
точки А к точке В. Кроме этой кривой на плоскости заданы две функции 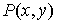 и и 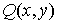 , которые определены, по крайней мере, на кривой АВ. , которые определены, по крайней мере, на кривой АВ.
Снова разобьем кривую АВ на части точками 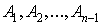 и пусть снова и пусть снова 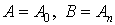 и и 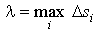 . Но теперь с дугой . Но теперь с дугой 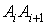 свяжем еще две
величины (см. рис. 9.2). свяжем еще две
величины (см. рис. 9.2).

Рис. 9.1 К построению понятия
криволинейного интеграла второго рода
Пусть 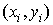 есть координаты
точки есть координаты
точки 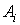 , и , и 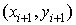 есть координаты
точки есть координаты
точки 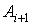 . Обозначим через . Обозначим через 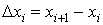 и и 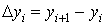 величины
проекций дуги величины
проекций дуги 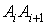 на оси OX и OY. Отметим,
что эти проекции имеют знак: если на оси OX и OY. Отметим,
что эти проекции имеют знак: если 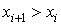 , то , то 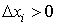 если же если же 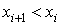 , то , то 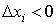 . То же самое можно сказать и о проекции . То же самое можно сказать и о проекции 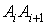 на ось OY. на ось OY.
Как и раньше выберем на куске кривой 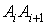 произвольным
образом среднюю точку произвольным
образом среднюю точку 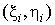 и составим уже две интегральные суммы и составим уже две интегральные суммы
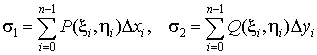 . .
Отметьте отличие
этих интегральных сумм от интегральной суммы криволинейного интеграла первого
рода: там стоит длина дуги 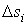 , а здесь – величины проекции этой дуги на оси
координат. , а здесь – величины проекции этой дуги на оси
координат.
Наконец, сделаем предельный переход 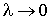 ; если существуют ; если существуют 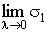 и и 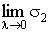 , и они не зависят от способа разбиения кривой АВ на кусочки и от способа выбора
средней точки, то они называются криволинейными интегралами второго рода , и они не зависят от способа разбиения кривой АВ на кусочки и от способа выбора
средней точки, то они называются криволинейными интегралами второго рода
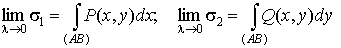 . .
Сумма этих
интегралов называется криволинейным интегралом второго рода общего вида и
обозначается символом
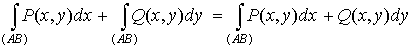 . .
Совершенно аналогично определяется
криволинейный интеграл второго рода по пространственной кривой
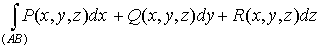 . .
Заметим, что если кривую АВ пройти в обратном направлении, от
точки В к точке А, то все проекции сменят знак; поэтому и интеграл сменит знак:
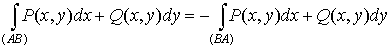 . .
9.2.2 Векторная
форма записи. Физический смысл
Рассмотрим
криволинейные интегралы второго рода по пространственной кривой
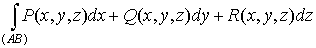 . .
Рассмотрим так
называемую вектор-функцию
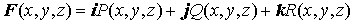
как трехмерный
вектор с компонентами 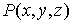 , , 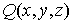 и и 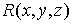 , а также вектор , а также вектор 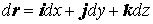 . Тогда комбинация, стоящая под знаком интеграла, есть
не что иное, как скалярное произведение . Тогда комбинация, стоящая под знаком интеграла, есть
не что иное, как скалярное произведение 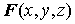 и и 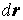 , то есть , то есть
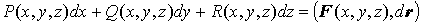 , ,
и поэтому
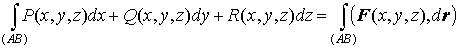 . .
Физически вектор-функция 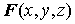 ассоциируется с
силовым полем, когда в каждой точке
пространства на материальную точку действует сила ассоциируется с
силовым полем, когда в каждой точке
пространства на материальную точку действует сила 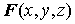 . Примером такого поля может служить гравитационное
поле, электрическое поле, магнитное поле и т.д. Физически скалярное
произведение . Примером такого поля может служить гравитационное
поле, электрическое поле, магнитное поле и т.д. Физически скалярное
произведение 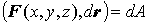 имеет смысл работы, которую силовое поле имеет смысл работы, которую силовое поле 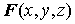 совершает,
перемещая материальную точку по вектору dr. Поэтому, с точки зрения физика, криволинейный
интеграл второго рода совершает,
перемещая материальную точку по вектору dr. Поэтому, с точки зрения физика, криволинейный
интеграл второго рода
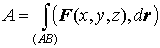
есть работа, которую совершает силовое поле 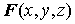 , перемещая материальную точку по кривой АВ. , перемещая материальную точку по кривой АВ.
Обозначим через a, b и g углы, которые вектор 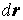 образует с
осями OX, OY и OZ. Заметим, что длина вектора образует с
осями OX, OY и OZ. Заметим, что длина вектора 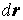
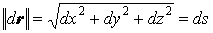
есть не что
иное, как дифференциал длины дуги кривой. Поэтому
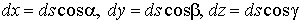
и мы можем
записать
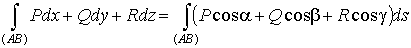 . .
Заметим, что
слева стоит криволинейный интеграл второго рода, а справа – криволинейный
интеграл первого рода. Эта формула, таким образом, дает связь между
криволинейными интегралами первого и второго рода.
9.2.3 Вычисление
криволинейных интегралов второго рода
Пусть
плоская кривая задана параметрически в виде 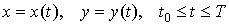 . Тогда . Тогда
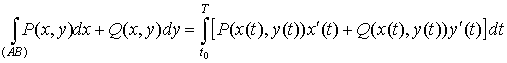 . .
Аналогичная
формула имеет место и для криволинейного интеграла по пространственной кривой.
9.3 Независимость
криволинейного интеграла от пути
Среди
силовых полей в физике особую роль играют так называемые потенциальные силовые поля. Их отличительной особенностью является
то, что работа, совершаемая таким полем, зависит лишь от начальной и конечной
точек пути, и не зависит от траектории, соединяющей эти точки. Математически
это соответствует тому, что криволинейный интеграл второго рода также зависит
лишь от начальной и конечной точек пути, и не зависит от траектории, соединяющей
эти точки. Поэтому с математической точки зрения представляет интерес выяснение
тех условий, при выполнении которых криволинейный интеграл обладает этим
свойством.
9.3.1 Плоский
случай
Пусть
дан криволинейный интеграл второго рода по плоской кривой
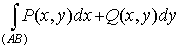 . .
Ответ на
поставленный вопрос дают следующие две теоремы.
Теорема
1. Для того чтобы 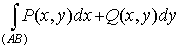 не зависел от
пути интегрирования необходимо и достаточно, чтобы существовала такая функция не зависел от
пути интегрирования необходимо и достаточно, чтобы существовала такая функция 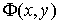 , что , что
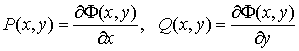 . .
Теорема
2. Если в односвязной области существуют и непрерывны 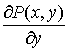 и и 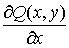 , то для того, чтобы было выполнено условие теоремы 1,
необходимо и достаточно, чтобы , то для того, чтобы было выполнено условие теоремы 1,
необходимо и достаточно, чтобы
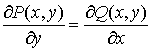 . .
9.3.2 Пространственный
случай
В
случае интегралов по пространственной кривой соответствующие теоремы
приобретают следующий вид.
Теорема
1. Для того чтобы 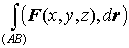 не зависел от
пути интегрирования необходимо и достаточно, чтобы существовала такая функция, не зависел от
пути интегрирования необходимо и достаточно, чтобы существовала такая функция, 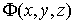 что что 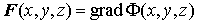 . .
Для формулировки второй теоремы введем
понятие ротора векторной функции.
Пусть 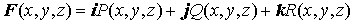 . Тогда ротор
этой функции определяется так: . Тогда ротор
этой функции определяется так:
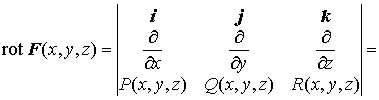
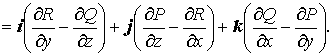
Теорема 2. Для того чтобы 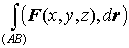 не зависел от
пути интегрирования необходимо и достаточно, чтобы выполнялось условие не зависел от
пути интегрирования необходимо и достаточно, чтобы выполнялось условие
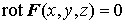 . .
9.4 Двойные интегралы
9.4.1 Определение
двойного интеграла
Пусть
на плоскости XOY заданы:
1. Некоторая
область D;
2. Функция двух переменных
f(x, y),
определенная, по крайней мере, в области D.
Проделаем построение, типичное для
определенного интеграла (см. рис.9.3).
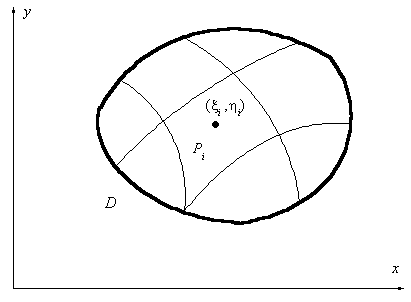
Рис. 9.3 К построению понятия
двойного интеграла
1. Разобьем
область D на части кривыми, имеющими площадь
0. С каждым кусочком свяжем следующие величины:
а)
площадь  i-го кусочка (сам кусочек будем обозначать ( i-го кусочка (сам кусочек будем обозначать (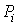 )); ));
б) величину 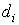 , называемую диаметром
этого кусочка, и определяемую как , называемую диаметром
этого кусочка, и определяемую как
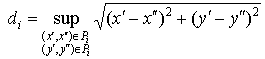 . .
По сути дела, 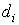 есть
максимальное расстояние между точками i-го кусочка области D. есть
максимальное расстояние между точками i-го кусочка области D.
в) наконец, введем величину 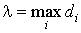 . .
2. На каждом кусочке произвольным
образом выберем некоторую точку 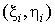 , которую будем называть «средней точкой», и составим
интегральную сумму , которую будем называть «средней точкой», и составим
интегральную сумму
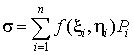 . .
3. Сделаем предельный переход 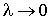 . Если существует . Если существует 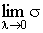 и этот предел
не зависит от способа разбиения области D на части от способа
выбора средней точки, то он называется двойным интегралом от функции и этот предел
не зависит от способа разбиения области D на части от способа
выбора средней точки, то он называется двойным интегралом от функции 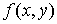 по области D и обозначается так по области D и обозначается так
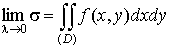 . .
9.4.2 Свойства
двойного интеграла
Ниже приведены основные свойства
двойного интеграла.
1. 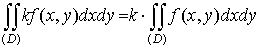 ; ;
2. 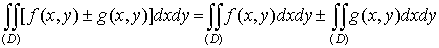 ; ;
3. Если 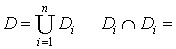 Æ при i ¹j, то Æ при i ¹j, то
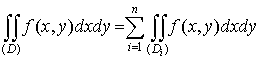 ; ;
4. 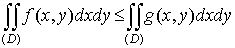 ; ;
5. 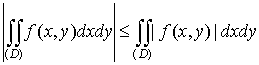 ; ;
6. Если 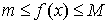 , то , то 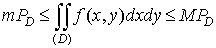 , где , где 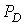 - площадь области
D; - площадь области
D;
7. Если 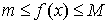 , то существует m такое, что , то существует m такое, что 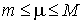 и и
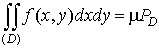 . .
В частности,
если 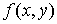 непрерывна в
области D, то существует точка непрерывна в
области D, то существует точка 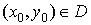 такая что такая что
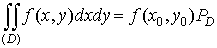 . .
9.4.3 Вычисление
двойных интегралов
Приведем лишь формулу для вычисления
двойных интегралов по области в виде криволинейной трапеции (см. рис. 9.4).
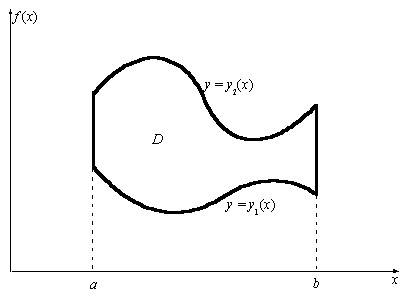
Рис. 9.4 Область интегрирования в
виде криволинейной трапеции
Теорема. Если существует 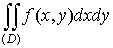 и и 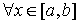 существует существует 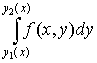 , то существует , то существует 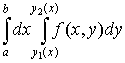 и имеет место
равенство и имеет место
равенство
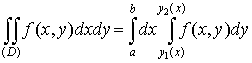 . .
9.4.4 Формула
Грина
Пусть имеется односвязная область D окруженная контуром L. Пусть в этой области определены две функции 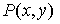 и и  , имеющие непрерывные производные , имеющие непрерывные производные 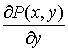 и и 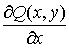 (см. рис. 9.5). (см. рис. 9.5).
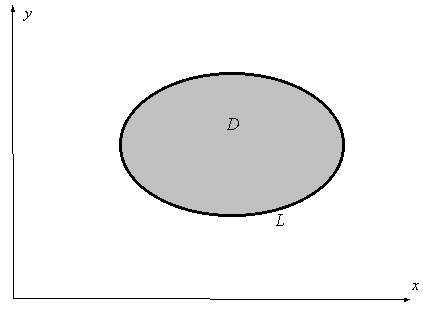
Рис. 9.5 Иллюстрация к формуле Грина
Тогда имеет
место формула
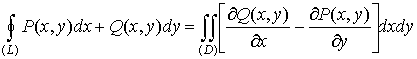 , ,
называемая формулой Грина. Она дает связь между
криволинейным интегралом второго рода по замкнутому контуру (символ 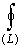 означает
криволинейный интеграл по замкнутому контуру; при этом считается, что контур
обходится так, что его внутренняя часть находится слева) и двойным интегралом
по области, которую этот контур ограничивает. означает
криволинейный интеграл по замкнутому контуру; при этом считается, что контур
обходится так, что его внутренняя часть находится слева) и двойным интегралом
по области, которую этот контур ограничивает.
9.4.5 Замена
переменных в двойном интеграле
Пусть нам необходимо вычислить двойной интеграл
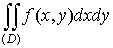 по некоторой
области D. Для возможного упрощения
вычислений сделаем замену переменных по некоторой
области D. Для возможного упрощения
вычислений сделаем замену переменных 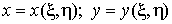 , переходя от «старых» переменных x, y к «новым» переменным x, h. В
дальнейшем будем предполагать, что , переходя от «старых» переменных x, y к «новым» переменным x, h. В
дальнейшем будем предполагать, что 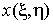 и и 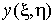 непрерывны и
имеют непрерывные частные производные по x и h. Кроме того,
предполагается, что эта система может быть однозначно разрешена относительно x и h: непрерывны и
имеют непрерывные частные производные по x и h. Кроме того,
предполагается, что эта система может быть однозначно разрешена относительно x и h: 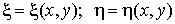 , то есть соответствие , то есть соответствие 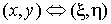 взаимно однозначное. взаимно однозначное.
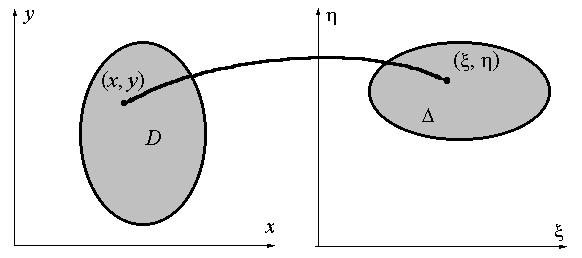
Рис. 9.6 Соответствие областей D и D
Тогда система 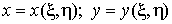 каждой точке каждой точке 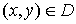 ставит в соответствие
точку ставит в соответствие
точку 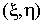 на плоскости xOh,
и это соответствие взаимно однозначное. Тем самым область D отображается в некоторую область D на плоскости xOh. на плоскости xOh,
и это соответствие взаимно однозначное. Тем самым область D отображается в некоторую область D на плоскости xOh.
Сама формула замены переменных в
двойном интеграле имеет вид
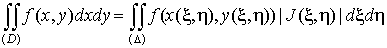 , ,
где величина 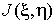 равна равна
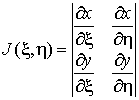 . .
Она называется якобианом перехода от переменных x, y к
переменным x,
h.
|